Ortogonal koordinatlar

Matematik'te, ortogonal koordinatlar q = (q¹, q², ..., q^d) bir d koordinat kümesi olarak tanımlanır,hepsi koordinat yüzeyi içinde dik açılarla birleşir(not: üstsimge indis'tir, üstel değildir).Özel bir koordinat için Bir koordinat yüzeyi q^k eğrilik, yüzey, veya hiperyüzey veya hangisiyse q_k bir sabittir. örneğin, üç-boyut Kartezyen koordinatlar (x, y, z) bir ortogonal koordinat sistemidir. Bu koordinat yüzeyleri için x = sabit, y = sabit, ve z = sabit.,yüzeyler dik açıda buluşurlar,bu örnek dik açı içindir. Ortogonal koordinatlar eğrisel koordinatlar'ın özel ama son derece yaygın bir durumudur.

Kartezyen olmayan koordinatların baş avantajı problemin simetri eşleştirmek için seçilebilir olmasıdır. Örneğin,bir patlama nedeniyle basınç dalgası Kartezyen koordinatlarda 3 boyutlu uzaya bağlıdır zemin (ya da diğer engeller) gibi,ancak basınç ağırlıklı olarak küresel koordinatlar sorunu çok olur, böylece,küresel koordinatlar'da öylesine sorun haline gelirki yaklaşık olarak bir boyutlu olur(bu basınç dalgası baskısı sadece merkezden zaman ve mesafeye bağlı olduğundan). Başka bir örnek düz bir dairesel borudaki (yavaş) bir sıvıdır: Kartezyen koordinatlarda, bir kısmi diferansiyel denklem içeren bir (zor) iki boyutlu sınır değer sorunu çözmek için vardır, fakat silindirik koordinatlar sorunu ile tek boyutlu olur bir kısmi diferansiyel denklemin yerini,düzgün diferansiyel denklemi alır.

Alıştırma

konformal haritada dörtgen gridler etkilidir .Eğimli gridlerin ortogonalitesinin korunduğunu unutmayın.

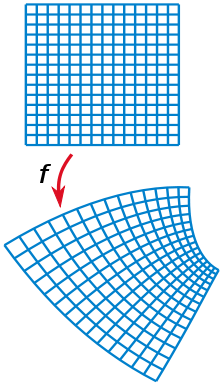
Vektör işlemleri ve fiziksel yasalar normalde Kartezyen koordinatlar'da kolay olsa da non-kartezyen ortogonal koordinatlar sıklıka farklı problemlerin çözümünde kullanılır,kuantum mekaniğinin alan teorisi, akışkan, elektrodinamik ve kimyasal türlerin difuzyon'u veya ısı'da bu gibi ortaya çıkan özellikle sınır değer probleminde..

Kartezyen olmayan koordinatların baş avantajı problemin simetri eşleştirmek için seçilebilir olmasıdır. Örneğin,bir patlama nedeniyle basınç dalgası Kartezyen koordinatlarda 3 boyutlu uzaya bağlıdır zemin (ya da diğer engeller) gibi,ancak basınç ağırlıklı olarak küresel koordinatlar sorunu çok olur, böylece küresel koordinatlar'da öylesine sorun haline gelirki yaklaşık olarak bir boyutlu olur(bu basınç dalgası baskısı sadece merkezden zaman ve mesafeye bağlı olduğundan). Başka bir örnek düz bir dairesel borudaki (yavaş) bir sıvıdır: Kartezyen koordinatlarda, bir kısmi diferansiyel denklem içeren bir (zor) iki boyutlu sınır değer sorunu çözmek için vardır, fakat silindirik koordinatlar sorunu ile tek boyutlu olur bir kısmi diferansiyel denklemin yerini düzgün diferansiyel denklemi alır.

Ortogonal koordinatların tercih nedeni genel eğrisel koordinatlar'ın basitleşirilebilmesidir: koordinatları ortogonal olmadığı durumlarda birçok komplikasyonlar ortaya çıkar. örneğin birçok problem,ortogonal koordinatlarda değişkenlerin ayrılması ile çözülür. Değişkenlere ayırma bir matematik tekniktir bir kompleksd-boyutlu problem, d tek-boyutlu problemlere dönüştürülerek bilinen fonksiyonun içindeki terimler çözülebilir. Birçok denklem Laplace denklemi veya Helmholtz denklemine indirgenebilir. Laplace denklemi ile 13 ortogonal koordinat sistemine ve Helmholtz denklemi ile 11 ortogonal koordinat sistemine ayrılır. ^[1][2]

Metrik tensör içindeki off-diagonal terimler asla ortogonal koordinatlar değildirler Diğer bir deyişle, sonsuz kare uzunluğu ds2 her zaman kare sonsuz koordinat yer değiştirmelerinin bir ölçekli toplamı olarak yazılabilir

${\displaystyle ds^{2}=\sum _{k=1}^{d}\left(h_{k}\,dq^{k}\right)^{2}}$

burada d boyuttur ve ölçek fonksiyonudur (veya ölçek faktörüdür)

${\displaystyle h_{k}(\mathbf {q} )\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {g_{kk}(\mathbf {q} )}}=|\mathbf {e} _{k}|}$

metrik tensör çapraz bileşenlerinin karekök veya aşağıda açıklanan yerel bazda vektörlerin ${\displaystyle \mathbf {e} _{k}}$ uzunlukları eşittir.

Burada ölçekleme fonksiyonu h_i yeni koordinatlarda,gradient,Laplacian, diverjans ve curl. gibi diferansiyel operatörleri hesaplamak için kullanılıyor Kartezyen koordinat (x, y) standart bir iki boyutlu grid konformal haritalaması iki boyutlu ortogonal koordinat sistemleri üretmek için basit bir yöntemdir. Bir karmaşık sayı z = x + iy, gerçek koordinatlar x ve y ile oluşturulabilmektedir.i kare kök -1'i temsil eder. ortaya çıkan karmaşık sayı w = u + iv olarak yazılmış ise herhangi bir holomorfik fonksiyonu w = f(z) sıfır olmayan karmaşık türev ile bir konformal haritalama üretecektir.Daha sonra sabit bir u ve v, sabit x ve y egrilerinin özgün çizgilerinin yaptığı gibi dik açıda kesişir. iki boyutlu bir koordinat sisteminden üç ve daha yüksek boyutlarda ortogonal koordinatlar ya da (silindirik koordinatlar) içine çıkıntı yapan ya da kendi simetri ekseni yaklaşık bir iki boyutlu bir sistem döndürülerek,ortogonal yeni bir boyut oluşturulabilir. Ancak, bu tür iki boyutlu bir sistemin, çıkıntı veya çevirerek elipsoidal koordinatlar elde edilemeyen üç boyutlu diğer ortogonal koordinat sistemleri vardır. Daha genel olarak dik koordinatlar bazı gerekli koordinat yüzeyleri ve dik yörüngeleri dikkate alınarak elde edilebilir.

Taban vektörler

Kovaryant taban

Kartezyen koordinatlar da taban vektörler(sabit) sabitlenir;daha genel çerçeve olan eğrisel koordinatlarda ise bu vektörler, uzayda nokta koordinatları ile belirtilir ve genellikle  bu tür noktalarla taban vektörler kümesi sabit değildir: Bu ​​genel olarak eğrisel koordinatlara özgüdür ve çok önemli bir kavramdır. ortogonal koordinatları ayıran temel vektörler farklı olsa da, her zaman birbirlerine göre ortogonal dir, yani diğer bir deyişle,

${\displaystyle \mathbf {e} _{i}\cdot \mathbf {e} _{j}=0\quad {\text{if}}\quad i\neq j}$

eğriliği tanjant vektörler tarafından tanımlanir ve bu taban vektörler diğerlerini sabit tutmak ve bir koordinati değiştirmek sureti ile elde edilir :

2D ortogonal koordinatların gösterimi. Sabit biri dışında tüm koordinat tutarak elde edilen eğriler, taban vektörler ile gösterilir, taban vektörlerin eşit uzunlukta olmadigi unutulmamalidir ve olmasıda gerekmez, sadece dik olması gerekir.

${\displaystyle \mathbf {e} _{i}={\frac {\partial \mathbf {r} }{\partial q^{i}}}}$

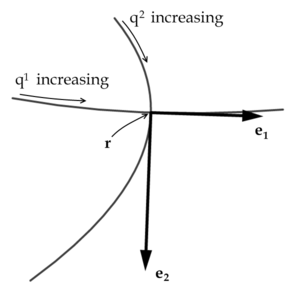
Burada r bir qⁱ noktasında taban vektörlerin elde edildiği koordinattır . Sabitlenmemiş koordinat bir parametrik eğri olarak zengindir ve parametreye (değişen koordinat) göre eğrinin türevi koordinatı oldugu için taban vektördür, başka bir deyişle, bir A eğrisi hariç tüm bir koordinat sabitleme ile elde edilmektedir Vektörlerin eşit uzunlukta olması gerekmediği unutulmamalidir,normalize taban vektörleri bir şapka ile noktaya ve uzunluğu ile bölünmesi ile elde edilir:

${\displaystyle {\hat {\mathbf {e} }}_{i}={\frac {\mathbf {e} _{i}}{\left|\mathbf {e} _{i}\right|}}}$

Bir vektör alanı baz vektörleri veya normalize baz vektörleri ile ilgili bileşenleri tarafından belirtilebilir. Normalize tabanda bileşenlerin niceliklerinde netlik (örneğin, bir teğet hız yerine teğet hız kez ölçek faktörü ile uğraşmak isteyebilirsiniz) uygulamalarin en yaygın, daha karmaşık olduğu türevlerde normalize tabanlarda daha az yaygın görülür . Kullanılan bu fonksiyonlar ölçek faktörü olarak bilinir (bazen Lamé katsayıları olarak adlandırılan,ve bu biraz daha iyi bilinen doğrusal elastisite içinde aynı adı taşıyan katsayilardan kaçinilmalidir) koordinatlarin basit uzunluğu taban vektörlerin uzunluğudur.(aşağıdaki tabloya bakınız).

Kontravaryant taban

Yukardaki taban vektörler kovaryant taban vektörler (çünkü bunlar birlikte "eş-değişir" vektörler)dir. Ortogonal koordinatlar, kontrvaryant taban vektörleri bildirdiğinden vektörleri aynı doğrultuda olarak karşılıklı uzunluğu bulmak kolaydır. (bu nedenle, birbirine göre iki taban vektörleri kümesinin karşılıklı olduğu söylenir ):

${\displaystyle \mathbf {e} ^{i}={\frac {{\hat {\mathbf {e} }}_{i}}{h_{i}}}={\frac {\mathbf {e} _{i}}{h_{i}^{2}}}}$

Bu, tanım gereğinin gerçek bir sonuçtur, ${\displaystyle \mathbf {e} _{i}\cdot \mathbf {e} ^{j}=\delta _{i}^{j}}$,Kronecker delta kullanılıyor.

${\displaystyle {\hat {\mathbf {e} }}_{i}={\frac {\mathbf {e} _{i}}{h_{i}}}=h_{i}\mathbf {e} ^{i}={\hat {\mathbf {e} }}^{i}}$

Şimdi yaygın olarak ortogonal koordinatlardaki üç farklı taban vektörlerini tanımlamak için kullanılan kümelerle karşı karşıyayiz: kovaryant taban e_i, kontravaryant taban eⁱ, ve normalize tabana êⁱ. Bir vektörün kimliği herhangi bir koordinat sisteminden bağımsız, yani bir nesnel miktar iken, diger bir vektörün vektör içeri bilesenleri gösterimi tabana bağlıdır. Kafa karışıklığını önlemek için, x vektörünün bileşenleri ile sırasıyla e_i taban gösterimi olarak xⁱ ve eⁱ taban gösterimi olarak x_i dir:

${\displaystyle \mathbf {x} =\sum _{i}x^{i}\mathbf {e} _{i}=\sum _{i}x_{i}\mathbf {e} ^{i}}$

İndis gösteriminin pozisyonu bileşenler ile şöyle hesaplanıyor(Üs üst indisi ile karıştırılmamalıdır). Burada toplam sembolünün Σ ( büyük sigma) olduğunu unutmayalım ve tüm vektörler üzerinden toplam olarak belirtilen (i = 1, 2, ..., d) sıklıkla ihmal edilir.Bileşenler basitçe aşağıdaki gibidir:

${\displaystyle h_{i}^{2}x^{i}=x_{i}\,}$

Normalize tabana göre herhangi bir vektör bileşeni için kullanılan yaygın indis gösterimi vardır, bu yazıda vektör bileşenleri için indisleri kullanma ve bileşenler normalize bazında nasıl hesaplanır buna dikkat edeceğiz..

Vektör cebri

Vektör ekleme ve olumsuzlama gibi herhangi bir komplikasyonda kartezyen koordinatlarda akıllı-bileşen olacaktır. Ekstra hususlar diğer vektör işlemleri için gerekli olabilir Tüm bu işlemler için,bir vektör alanında iki vektörün (diğer bir deyişle, vektörlerin kuyrukları denk) aynı noktaya bağlı olduğunun varsayıldığı unutulmamalıdır.İki vektör bileşenleri uzayda farklı noktalarda hesaplanarak ilave edildiği takdirde taban vektörler genel olarak, ortogonal koordinatlar değiştigi için, farklı taban vektörleri olarak düşünülmesi gerekir

Nokta çarpım

Kartezyen koordinatlarda nokta çarpım (Öklid uzayı ile ortonormal taban kümesi) basit bileşenlerin çarpımlarının toplamıdır.Dik koordinatlarda, x ve y iki vektörün nokta çarpım vektörlerin bileşenleri normalize bazında hesaplanan ailevi form halini alır:

${\displaystyle \mathbf {x} \cdot \mathbf {y} =\sum _{i}x_{i}{\hat {\mathbf {e} }}_{i}\cdot \sum _{j}y_{j}{\hat {\mathbf {e} }}_{j}=\sum _{i}x_{i}y_{i}}$

Bu noktada normalize edilmiş olarak ortonormal baz grubu bir Kartezyen koordinat sistemi oluşturma gerçeğinin bir sonucudur :

Kovaryant veya kontrvaryant tabanlardaki bileşenler için

${\displaystyle \mathbf {x} \cdot \mathbf {y} =\sum _{i}h_{i}^{2}x^{i}y^{i}=\sum _{i}{\frac {x_{i}y_{i}}{h_{i}^{2}}}=\sum _{i}x^{i}y_{i}=\sum _{i}x_{i}y^{i}}$

Bu kolaylıkla elde edilebilir, bileşen formu içindeki vektörleri dışarı yazma temelinde taban vektörleri normalize ve nokta çarpım alarak elde edilebilir. Örneğin, 2D:

${\displaystyle {\begin{aligned}\mathbf {x} \cdot \mathbf {y} &=\left(x^{1}\mathbf {e} _{1}+x^{2}\mathbf {e} _{2}\right)\cdot \left(y_{1}\mathbf {e} ^{1}+y_{2}\mathbf {e} ^{2}\right)\\[10pt]&=\left(x^{1}h_{1}{\hat {\mathbf {e} }}_{1}+x^{2}h_{2}{\hat {\mathbf {e} }}_{2}\right)\cdot \left(y_{1}{\frac {{\hat {\mathbf {e} }}^{1}}{h_{1}}}+y_{2}{\frac {{\hat {\mathbf {e} }}^{2}}{h_{2}}}\right)=x^{1}y_{1}+x^{2}y_{2}\end{aligned}}}$

burada normalize kontravaryant ve kovaryant üsleri eşit olduğu gerçeği kullanılmıştır

Çapraz çarpım

çapraz çarpım 3D kartezyen koordinatlarda:

${\displaystyle \mathbf {x} \times \mathbf {y} =(x_{2}y_{3}-x_{3}y_{2}){\hat {\mathbf {e} }}_{1}+(x_{3}y_{1}-x_{1}y_{3}){\hat {\mathbf {e} }}_{2}+(x_{1}y_{2}-x_{2}y_{1}){\hat {\mathbf {e} }}_{3}}$

bileşenleri normalize tabanda hesaplanır, yukarıdaki formül daha sonra ortogonal koordinatlarda geçerli kalır

Kovaryant veya kontravaryant üsleri ile dik koordinatlarda çapraz çarpımı oluşturmak için yine basitçe taban vektörlerin normalizesi gerekir Örneğin:

${\displaystyle \mathbf {x} \times \mathbf {y} =\sum _{i}x^{i}\mathbf {e} _{i}\times \sum _{j}y^{j}\mathbf {e} _{j}=\sum _{i}x^{i}h_{i}{\hat {\mathbf {e} }}_{i}\times \sum _{j}y^{j}h_{j}{\hat {\mathbf {e} }}_{j}}$

açılımı yazılırsa,

${\displaystyle \mathbf {x} \times \mathbf {y} =(x^{2}y^{3}-x^{3}y^{2}){\frac {h_{2}h_{3}}{h_{1}}}\mathbf {e} _{1}+(x^{3}y^{1}-x^{1}y^{3}){\frac {h_{1}h_{3}}{h_{2}}}\mathbf {e} _{2}+(x^{1}y^{2}-x^{2}y^{1}){\frac {h_{1}h_{2}}{h_{3}}}\mathbf {e} _{3}}$

Ortogonal olmayan koordinatların daha yüksek boyutlara basitleştirilmiş genellemesi çapraz çarpım için kısa ve öz gösterimi Levi-Civita tensörü ile mümkündür bu ölçek faktörlerin biri değilse diğer bileşenleri bir ve sıfır olacaktır.

Taban vektör formülleri

dr ve normalize edilmis taban vektörler ê_i den, aşağıda inşa edilmiştir.^[3][4]

değişken eleman	Vektörler	Skalerler
Doğrusal eleman	koordinat eğrisinin tanjant vektörü qi: ${\displaystyle d{\boldsymbol {\ell }}=h_{i}{\hat {\mathbf {e} }}_{i}={\frac {\partial \mathbf {r} }{\partial q_{i}}}}$	sonsuz uzunluk ${\displaystyle d\ell ={\sqrt {d\mathbf {r} \cdot d\mathbf {r} }}={\sqrt {h_{1}^{2}\,dq_{1}^{2}+h_{2}^{2}\,dq_{2}^{2}+h_{3}^{2}\,dq_{3}^{2}}}}$
yüzey elemanı	Normal koordinat yüzeyiqk = sabit: ${\displaystyle {\begin{aligned}d\mathbf {S} &=(h_{i}q_{i}{\hat {\mathbf {e} }}_{i})\times (h_{j}q_{j}{\hat {\mathbf {e} }}_{j})\\&=h_{i}h_{j}q_{i}q_{j}\left({\frac {\partial \mathbf {r} }{\partial q_{i}}}\times {\frac {\partial \mathbf {r} }{\partial q_{j}}}\right)\\&=h_{i}h_{j}q_{i}q_{j}{\hat {\mathbf {e} }}_{k}\end{aligned}}}$	sonsuzyüzey ${\displaystyle dS_{k}=h_{i}h_{j}\,dq^{i}\,dq^{j}}$
Hacim elemanı	N/A	sonsuz hacim ${\displaystyle {\begin{aligned}dV&=|(h_{1}\,dq_{1}{\hat {\mathbf {e} }}_{1})\cdot (h_{2}\,dq_{2}{\hat {\mathbf {e} }}_{2})\times (h_{3}\,dq_{3}{\hat {\mathbf {e} }}_{3})|\\&=|{\hat {\mathbf {e} }}_{1}\cdot {\hat {\mathbf {e} }}_{2}\times {\hat {\mathbf {e} }}_{3}|h_{1}h_{2}h_{3}\,dq_{1}\,dq_{2}\,dq_{3}\\&=J\,dq_{1}\,dq_{2}\,dq_{3}\\&=h_{1}h_{2}h_{3}\,dq_{1}\,dq_{2}\,dq_{3}\end{aligned}}}$

burada

${\displaystyle J=\left|{\frac {\partial \mathbf {r} }{\partial q_{1}}}\cdot \left({\frac {\partial \mathbf {r} }{\partial q_{2}}}\times {\frac {\partial \mathbf {r} }{\partial q_{3}}}\right)\right|=\left|{\frac {\partial (x,y,z)}{\partial (q_{1},q_{2},q_{3})}}\right|=h_{1}h_{2}h_{3}}$

Jacobian determinant tır, Bu hacimdeki deformasyondan sonsuzküçük küb dxdydz ye ortogonal koordinatlar içinde sonsuz eğrilik hacminin geometrik karşılaştırma idi.

İntegral

${\displaystyle \int _{\mathcal {P}}\mathbf {F} \cdot d\mathbf {r} =\int _{\mathcal {P}}\sum _{i}F_{i}\mathbf {e} ^{i}\cdot \sum _{j}\mathbf {e} _{j}\,dq^{j}=\sum _{i}\int _{\mathcal {P}}F_{i}\,dq^{i}}$

Bir koordinatla başlanıp açıklanan yüzey alanı için bir sonsuz eleman q_k sabittir:

${\displaystyle dA=\prod _{i\neq k}ds_{i}=\prod _{i\neq k}h_{i}\,dq^{i}\,}$

Benzer şekilde, hacim elemanı:

${\displaystyle dV=\prod _{i}ds_{i}=\prod _{i}h_{i}\,dq^{i}}$

Burada büyük Π indisi (sapkali Pi) bir çarpım benzer sekilde büyük Σ indisi toplam sembolüdür. Unutmadan tüm ölçek faktörlerinin çarpimlari Jakobiyen determinanttir.

Bir örnek olarak bir vektör fonksiyonu F in üzerinde q¹ = sabit yüzey 3D içinde ${\displaystyle \scriptstyle {\mathcal {S}}}$ yüzeysel integral i  :

${\displaystyle \int _{\mathcal {S}}\mathbf {F} \cdot d\mathbf {A} =\int _{\mathcal {S}}\mathbf {F} \cdot {\hat {\mathbf {n} }}\ dA=\int _{\mathcal {S}}\mathbf {F} \cdot {\hat {\mathbf {e} }}_{1}\ dA=\int _{\mathcal {S}}F^{1}{\frac {h_{2}h_{3}}{h_{1}}}\,dq^{2}\,dq^{3}}$

dir Not olarak F¹/h₁ normal yüzeyinin F bileşenidir .

Üç boyutlu diferansiyel operatörler

Bu işlemler uygulamada yaygın olduğu için, bu bölümdeki tüm vektör bileşenleri normalize esasına göre sunulmaktadır.

Operator	Expression
bir skaler alan Gradyan	${\displaystyle \nabla \phi ={\frac {{\hat {\mathbf {e} }}_{1}}{h_{1}}}{\frac {\partial \phi }{\partial q^{1}}}+{\frac {{\hat {\mathbf {e} }}_{2}}{h_{2}}}{\frac {\partial \phi }{\partial q^{2}}}+{\frac {{\hat {\mathbf {e} }}_{3}}{h_{3}}}{\frac {\partial \phi }{\partial q^{3}}}}$
bir vektör alanı'nın Diverjans'ı	${\displaystyle \nabla \cdot \mathbf {F} ={\frac {1}{h_{1}h_{2}h_{3}}}\left[{\frac {\partial }{\partial q^{1}}}\left(F_{1}h_{2}h_{3}\right)+{\frac {\partial }{\partial q^{2}}}\left(F_{2}h_{3}h_{1}\right)+{\frac {\partial }{\partial q^{3}}}\left(F_{3}h_{1}h_{2}\right)\right]}$
Bir vektör alanının Curl	${\displaystyle {\begin{aligned}\nabla \times \mathbf {F} &={\frac {{\hat {\mathbf {e} }}_{1}}{h_{2}h_{3}}}\left[{\frac {\partial }{\partial q^{2}}}\left(h_{3}F_{3}\right)-{\frac {\partial }{\partial q^{3}}}\left(h_{2}F_{2}\right)\right]+{\frac {{\hat {\mathbf {e} }}_{2}}{h_{3}h_{1}}}\left[{\frac {\partial }{\partial q^{3}}}\left(h_{1}F_{1}\right)-{\frac {\partial }{\partial q^{1}}}\left(h_{3}F_{3}\right)\right]\\[10pt]&+{\frac {{\hat {\mathbf {e} }}_{3}}{h_{1}h_{2}}}\left[{\frac {\partial }{\partial q^{1}}}\left(h_{2}F_{2}\right)-{\frac {\partial }{\partial q^{2}}}\left(h_{1}F_{1}\right)\right]={\frac {1}{h_{1}h_{2}h_{3}}}{\begin{vmatrix}h_{1}{\hat {\mathbf {e} }}_{1}&h_{2}{\hat {\mathbf {e} }}_{2}&h_{3}{\hat {\mathbf {e} }}_{3}\\{\dfrac {\partial }{\partial q^{1}}}&{\dfrac {\partial }{\partial q^{2}}}&{\dfrac {\partial }{\partial q^{3}}}\\h_{1}F_{1}&h_{2}F_{2}&h_{3}F_{3}\end{vmatrix}}\end{aligned}}}$
Bir skaler alanın Laplasyen i	${\displaystyle \nabla ^{2}\phi ={\frac {1}{h_{1}h_{2}h_{3}}}\left[{\frac {\partial }{\partial q^{1}}}\left({\frac {h_{2}h_{3}}{h_{1}}}{\frac {\partial \phi }{\partial q^{1}}}\right)+{\frac {\partial }{\partial q^{2}}}\left({\frac {h_{3}h_{1}}{h_{2}}}{\frac {\partial \phi }{\partial q^{2}}}\right)+{\frac {\partial }{\partial q^{3}}}\left({\frac {h_{1}h_{2}}{h_{3}}}{\frac {\partial \phi }{\partial q^{3}}}\right)\right]}$

Ortogonal koordinatlar tablosu

Her zamanki kartezyen koordinat yanı sıra, birkaç diğerleri aşağıda verilmiştir.^[4] Aralıklı gösterim koordinatların sütunda yer kaplaması için kullanılır.

Eğrisel koordinatlar (q1, q2, q3)	Kartezyenden dönüşüm(x, y, z)	ölçek çarpanı
Küresel kutupsal koordinatlar ${\displaystyle (r,\theta ,\phi )\in [0,\infty )\times [0,\pi ]\times [0,2\pi )}$	${\displaystyle {\begin{aligned}x&=r\sin \theta \cos \phi \\y&=r\sin \theta \sin \phi \\z&=r\cos \theta \end{aligned}}}$	${\displaystyle {\begin{aligned}h_{1}&=1\\h_{2}&=r\\h_{3}&=r\sin \theta \end{aligned}}}$
Silindrik kutupsal koordinatlar ${\displaystyle (r,\phi ,z)\in [0,\infty )\times [0,2\pi )\times (-\infty ,\infty )}$	${\displaystyle {\begin{aligned}x&=r\cos \phi \\y&=r\sin \phi \\z&=z\end{aligned}}}$	${\displaystyle {\begin{aligned}h_{1}&=h_{3}=1\\h_{2}&=r\end{aligned}}}$
Parabolik silindrik koordinatlar ${\displaystyle (u,v,z)\in (-\infty ,\infty )\times [0,\infty )\times (-\infty ,\infty )}$	${\displaystyle {\begin{aligned}x&={\frac {1}{2}}(u^{2}-v^{2})\\y&=uv\\z&=z\end{aligned}}}$	${\displaystyle {\begin{aligned}h_{1}&=h_{2}={\sqrt {u^{2}+v^{2}}}\\h_{3}&=1\end{aligned}}}$
Paraboloidal koordinatlar ${\displaystyle (u,v,\phi )\in [0,\infty )\times [0,\infty )\times [0,2\pi )}$	${\displaystyle {\begin{aligned}x&=uv\cos \phi \\y&=uv\sin \phi \\z&={\frac {1}{2}}(u^{2}-v^{2})\end{aligned}}}$	${\displaystyle {\begin{aligned}h_{1}&=h_{2}={\sqrt {u^{2}+v^{2}}}\\h_{3}&=uv\end{aligned}}}$
Eliptik silindrik koordinatlar ${\displaystyle (u,v,z)\in [0,\infty )\times [0,2\pi )\times (-\infty ,\infty )}$	${\displaystyle {\begin{aligned}x&=a\cosh u\cos v\\y&=a\sinh u\sin v\\z&=z\end{aligned}}}$	${\displaystyle {\begin{aligned}h_{1}&=h_{2}=a{\sqrt {\sinh ^{2}u+\sin ^{2}v}}\\h_{3}&=1\end{aligned}}}$
Yayvan küresel koordinatlar ${\displaystyle (\xi ,\eta ,\phi )\in [0,\infty )\times [0,\pi ]\times [0,2\pi )}$	${\displaystyle {\begin{aligned}x&=a\sinh \xi \sin \eta \cos \phi \\y&=a\sinh \xi \sin \eta \sin \phi \\z&=a\cosh \xi \cos \eta \end{aligned}}}$	${\displaystyle {\begin{aligned}h_{1}&=h_{2}=a{\sqrt {\sinh ^{2}\xi +\sin ^{2}\eta }}\\h_{3}&=a\sinh \xi \sin \eta \end{aligned}}}$
Yatık küresel koordinatlar ${\displaystyle (\xi ,\eta ,\phi )\in [0,\infty )\times \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\times [0,2\pi )}$	${\displaystyle {\begin{aligned}x&=a\cosh \xi \cos \eta \cos \phi \\y&=a\cosh \xi \cos \eta \sin \phi \\z&=a\sinh \xi \sin \eta \end{aligned}}}$	${\displaystyle {\begin{aligned}h_{1}&=h_{2}=a{\sqrt {\sinh ^{2}\xi +\sin ^{2}\eta }}\\h_{3}&=a\cosh \xi \cos \eta \end{aligned}}}$
Elipsoidal koordinatlar ${\displaystyle {\begin{aligned}&(\lambda ,\mu ,\nu )\\&\lambda <c^{2}<b^{2}<a^{2},\\&c^{2}<\mu <b^{2}<a^{2},\\&c^{2}<b^{2}<\nu <a^{2},\end{aligned}}}$	${\displaystyle {\frac {x^{2}}{a^{2}-q_{i}}}+{\frac {y^{2}}{b^{2}-q_{i}}}+{\frac {z^{2}}{c^{2}-q_{i}}}=1}$ where ${\displaystyle (q_{1},q_{2},q_{3})=(\lambda ,\mu ,\nu )}$	${\displaystyle h_{i}={\frac {1}{2}}{\sqrt {\frac {(q_{j}-q_{i})(q_{k}-q_{i})}{(a^{2}-q_{i})(b^{2}-q_{i})(c^{2}-q_{i})}}}}$
Bipolar koordinatlar ${\displaystyle (u,v,z)\in [0,2\pi )\times (-\infty ,\infty )\times (-\infty ,\infty )}$	${\displaystyle {\begin{aligned}x&={\frac {a\sinh v}{\cosh v-\cos u}}\\y&={\frac {a\sin u}{\cosh v-\cos u}}\\z&=z\end{aligned}}}$	${\displaystyle {\begin{aligned}h_{1}&=h_{2}={\frac {a}{\cosh v-\cos u}}\\h_{3}&=1\end{aligned}}}$
Toroidal koordinatlar ${\displaystyle (u,v,\phi )\in (-\pi ,\pi ]\times [0,\infty )\times [0,2\pi )}$	${\displaystyle {\begin{aligned}x&={\frac {a\sinh v\cos \phi }{\cosh v-\cos u}}\\y&={\frac {a\sinh v\sin \phi }{\cosh v-\cos u}}\\z&={\frac {a\sin u}{\cosh v-\cos u}}\end{aligned}}}$	${\displaystyle {\begin{aligned}h_{1}&=h_{2}={\frac {a}{\cosh v-\cos u}}\\h_{3}&={\frac {a\sinh v}{\cosh v-\cos u}}\end{aligned}}}$
Konikal koordinatlar ${\displaystyle {\begin{aligned}&(\lambda ,\mu ,\nu )\\&\nu ^{2}<b^{2}<\mu ^{2}<a^{2}\\&\lambda \in [0,\infty )\end{aligned}}}$	${\displaystyle {\begin{aligned}x&={\frac {\lambda \mu \nu }{ab}}\\y&={\frac {\lambda }{a}}{\sqrt {\frac {(\mu ^{2}-a^{2})(\nu ^{2}-a^{2})}{a^{2}-b^{2}}}}\\z&={\frac {\lambda }{b}}{\sqrt {\frac {(\mu ^{2}-b^{2})(\nu ^{2}-b^{2})}{a^{2}-b^{2}}}}\end{aligned}}}$	${\displaystyle {\begin{aligned}h_{1}&=1\\h_{2}^{2}&={\frac {\lambda ^{2}(\mu ^{2}-\nu ^{2})}{(\mu ^{2}-a^{2})(b^{2}-\mu ^{2})}}\\h_{3}^{2}&={\frac {\lambda ^{2}(\mu ^{2}-\nu ^{2})}{(\nu ^{2}-a^{2})(\nu ^{2}-b^{2})}}\end{aligned}}}$

Ayrıca bakınız

• Eğrisel koordinatlar
• Tensör
• Vektör alanı
• Çarpık koordinatlar

Şablon:Orthogonal coordinate systems

Notlar

1. Eric W. Weisstein. "Orthogonal Coordinate System". MathWorld. 12 Kasım 2014 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20141112082257/http://mathworld.wolfram.com/OrthogonalCoordinateSystem.html. Erişim tarihi: 10 July 2008. 
2. Morse and Feshbach 1953, Volume 1, pp. 494-523, 655-666.
3. Mathematical Handbook of Formulas and Tables (3rd edition), S. Lipschutz, M.R. Spiegel, J. Liu, Schuam's Outline Series, 2009, ISBN 978-0-07-154855-7.
4. Vector Analysis (2nd Edition), M.R. Spiegel, S. Lipschutz, D. Spellman, Schaum’s Outlines, McGraw Hill (USA), 2009, ISBN 978-0-07-161545-7

Kaynakça

• Korn GA ve Korn TM. (1961), Mathematical Handbook for Scientists and Engineers, McGraw-Hill, ss. 164–182 
• Morse & Feshbach (1953), Methods of Theoretical Physics, Volume 1, McGraw-Hill 
• Margenau H. ve Murphy GM. (1956), The Mathematics of Physics and Chemistry, 2. basım, Van Nostrand,, ss. 172–192 
• Leonid P. Lebedev ve Michael J. Cloud (2003), Tensor Analysis, ss. 81–88