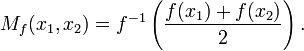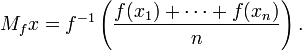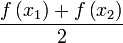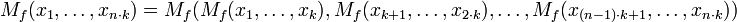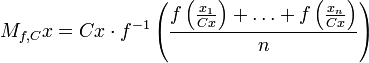Genelleştirilmiş f-ortalaması

Matematik ve istatistik bilim dallarında genelleştirilmiş f-ortalaması merkezsel konum ölçülerinden olan değişik ortalamalar için tek bir genel fonksiyon ve formül bulma ve kullanma çabaları sonucu ortaya çıkarılmıştır. Benzer çabalar biraz değişik diğer bir genelleştirilmiş ortalama formülünü vermiştir.^[1]. Bu nedenle isim karışıklığını önlemek için f-ortalaması çeşitli diğer isimlerde de anılmaktadır. Bazan yarı-aritmetik ortalama adı kullanılmaktadır. Bu kavramı ve formülü ilk geliştiren Rus matematikçisi A.Kolmogorov adına atfen de bazan Kolmogorov ortalaması olarak isimlendirilmektedir.^[2]

Tanımlama

Eğer f, reel doğrunun bağlanmış altseti olan 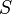$S$yi reel sayılara tasarımlayan bir fonksiyon ise ve hem sürekli hem de enjektif ise, o halde şu iki sayı olan 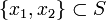$\{x_1, x_2\} \subset S$ için f-ortalaması şöyle tanımlanır:

$M_f(x_1,x_2) = f^{-1}\left( \frac{f(x_1)+f(x_2)}2 \right).$

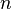$n$ büyüklükteki bir veri dizisi

$\{x_1, \dots, x_n\} \subset S$,

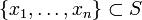olur ve f-ortalaması

$M_f x = f^{-1}\left( \frac{f(x_1)+ \cdots + f(x_n)}n \right).$

ifadesi ile verilir.

Ters fonksiyon olan 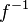$f^{-1}$ mevcut olması için fnin enjektif olması gerekir. Fonksiyonun sürekli olması için

$\frac{f\left(x_1\right) + f\left(x_2\right)}2$

ifadesinin 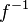$f^{-1}$ sahasında bulunmalıdır. Böylece enjektif ve sürekli olması sağlanan f kesinlikle monotonik fonksiyon olur ve bunun için 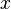$x$ içinde ne bu grubun içindeki en büyük sayıdan daha büyük ne de grubun en küçük sayısından daha küçük olabilir.

Özellikler

• Bölüntülenme: f-ortalama hesaplanırken, veriler birbirine eşit alt-bloklara bölüntülenebilip genel sonuca etki yapmadan hesaplar ayrı ayrı alt-bloklara uygulanabilir:

$M_f(x_1,\dots,x_{n\cdot k}) = M_f(M_f(x_1,\dots,x_{k}), M_f(x_{k+1},\dots,x_{2\cdot k}), \dots, M_f(x_{(n-1)\cdot k + 1},\dots,x_{n\cdot k}))$

• Elemanların çarpma özelliği korunursa, genel f-ortalamayı etkilemeden her altset için ayrı ortalama önceden hesaplanabilir.

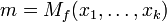$m=M_f(x_1,\dots,x_{k})$ ile şu ifade gerçek olabilir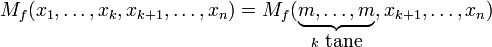

$M_f(x_1,\dots,x_{k},x_{k+1},\dots,x_{n}) = M_f(\underbrace{m,\dots,m}_{k \mbox{ tane}},x_{k+1},\dots,x_{n})$

• Genelleştirilmiş f-ortalamasi 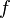$f$ de kaymalar ve yeniden ölçeklenmelerden etkilenmez; yani

$\forall a\ \forall b\ne0 ((\forall t\ g(t)=a+b\cdot f(t)) \Rightarrow \forall x\ M_f x = M_g x)$.

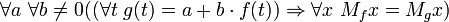• Eğer 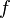$f$ monotonik ise, o halde 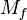$M_f$de monotoniktir.

İlişkiler

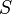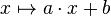• Eğer $S$ reel doğruya (yahut $a$nin sıfır olmadığı herhangi bir doğrusal fonksiyon $x\mapsto a\cdot x + b$a) tasarımlanırsa ve 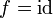$f = \mathrm{id}$, ise f-ortalaması aritmetik ortalama olur.
• Eğer 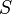$S$ pozitif reel sayılar setine tasarımlanırsa ve 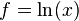$f = \ln(x)$, ise f-ortalaması geometrik ortalama olur. f-ortalaması özelliklere uygun olarak bu sonuç eğer pozitif ise ve 1 değilse, dayandığı logaritma bazının ne olduğunun hiç önemi bulunmamaktadır.
• Eğer 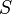$S$ pozitif reel sayılar setine tasarımlanırsa ve 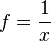$f = \frac{1}{x}$, ise f-ortalaması harmonik ortalama olur.
• Eğer 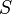$S$ pozitif reel sayılar setine tasarımlanırsa ve 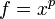$f = x^p$, ise f-ortalaması 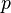$p$ üslü güç ortalaması olur.

Homojenlik

Ortalama için kullançılan fonksiyonlar ok kere homojendirler. Ancak f-ortalaması için 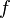$f$ fonksiyonlarının çoğu homojen değildir. Homojenlik özelliği girdi veri değerlerini özel bir homojen ortalama 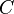$C$ ile normalize ederek yani

$M_{f,C} x = C x \cdot f^{-1}\left( \frac{f\left(\frac{x_1}{C x}\right) + \dots + f\left(\frac{x_n}{C x}\right)}{n} \right)$

sağlanabilir. Ancak bu değişme bazı f-ortalamaları için monotonluk ve bölüntülenme özelliklerin ortadan kaldırabilir.

İçsel kaynaklar

• Ortalama
• Genelleştirilmiş ortalama
• Jensen'in eşitsizliği

Referanslar

1. Bibby,J.(1974) "Axiomatisations of the average and a further generalisation of monotonic sequences," Glasgow Mathematical Journal, C. 15, say. 63–65
2. Kolmogorov,A. (1930) Mathematics and mechanics, Moskova say.136-138. (Rusça)