Eylemsizlik momenti

Eylemsizlik momenti
Cambazın elinde uzun bir çubuk var. Çubuğun uzun olması, onun eylemsizlik momentini arttırarak dönmeye karşı direnç oluşturur ve cambazın dengeyi sağlamasına yardımcı olur.
Yaygın sembol(ler):	I
SI birimi:	kg · m^2

Eylemsizlik momenti veya atalet momenti (SI birimi kilogram metrekare - kg·m²), dönme hareketi yapan bir cismin dönme eylemsizliğidir.

Tanım

Döner sandalye deneyi eylemsizlik momentini açıklar. Sandalyede dönen profesör kollarını açtığında eylemsizlik momenti azalır; açısal momentumu korumak için açısal hızı azalır. Deney Makedonya Üsküp Cyril ve Methodius Üniversitesinden Prof. Oliver Zajkov tarafından yapılmıştır.

Eylemsizlik momenti katı(bükülmez)cisimlerin, kendi rotasyon hareketlerindeki değişime karşı eylemsizliğini gösterir. Duran bir cismin eylemsizliği cismin kütlesi olduğu gibi, dönen bir cismin eylemsizliği de eylemsizlik momentidir. Eylemsizlik momenti kavramı iki başlık altında incelenir. Alan eylemsizlik momenti ve kütlesel eylemsizlik momenti:

1. Alan eylemsizlik momenti (Kesit/Polar atalet momenti): Rastgele seçilen bir koordinat sistemine göre bir cismin iki boyutu (yüzeyi) ele alınmış olsun. Bu yüzey, rastgele seçilen koordinat sisteminin bir eksenine dik olsun. Yüzeyin şekil değiştirmeme isteğinin yüzeyi içine alan eksenlere göre tanımlanmış haline alan eylemsizlik momenti denir. Cismin seçilen yüzeyine dik eksen z ekseni olsun. Yani incelenen düzlem x-y düzlemi üzerindedir. Bu şekliyle alan eylemsizlik momenti x eksenine ve y eksenine göre ayrı ayrı tanımlanabilir.
2. Eylemsizliğin bulunması istenen yüzey homojen ve tek boyutlu ise ${\displaystyle \lambda ={\frac {dM}{dL}}={\frac {M}{L}}}$; iki boyutlu ise ${\displaystyle \sigma ={\frac {dM}{dA}}={\frac {M}{A}}}$; üç boyutlu ise ${\displaystyle \rho ={\frac {dM}{dV}}={\frac {M}{V}}}$ kullanılır.
3. Alan eylemsizlik momenti formülü, malzemelerin burulması ve eğilmesiyle ilgili hesaplamalarda kullanılır. Özet olarak, yüzey şeklini değiştirmeye çalışan kuvvete koyduğu tepkidir. Birimi metre⁴ dür. Yani yüzeyin ufak bir değişimine olan tepki çok fazla yansıyacaktır.
4. Kütlesel Atalet Momenti: Hareketin çeşitli koordinat sistemlerinde( kartezyen koordinat sistemi, yarı kutupsal koordinat sistemi, doğal koordinat sistemi) vektörel olarak tanımlanmasıyla, yer vektörünün zamana göre iki kez türevi alınmasıyla ivmenin vektörel olarak büyüklüğü belirlenmiş olur. Bu ivmeye ait kütle eylemsizlik momenti oluşturur. Bu da ${\displaystyle F=m.a}$ formülasyonu ile gösterilmektedir.
5. Kütlesel atalet momentini tanımlamak için hareketli cismin dinamik (hareketli) ve statik(durgun) hallerdeki durumlarına uygun olan, cisim üzerinden noktalar belirlenmelidir.
6. Genel olarak statik cisimler tek noktaya indirgenir. Yani, durgun halde L uzunluğunda homojen bir silindirin ağırlık ve kütle merkezi olan tam ortasına indirgenir ve sanki cisim orada toplanmış gibi düşünülür. Fakat dönme veya salınım hareketi yaptığında bir noktaya göre tanımlamak bazı durumlarda dinamik özellikleri yansıtmayabilir. Bu nedenle, çubuğu iki noktaya ya da dönme veya salınım hızı arttıkça üç noktaya indirgenebilir. Hareketin karmaşıklığı arttıkça kütlenin indirgendiği nokta sayısı da arttırılabilir. Fakat dört noktadan fazlası problemin çözümünden sapmayı arttırır.

Eylemsizlik momenti örnekleri

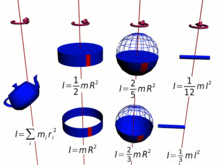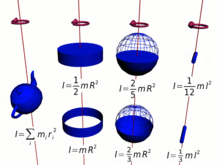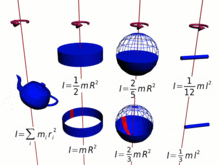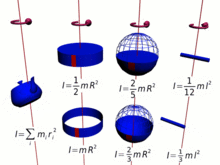
Hesaplanması

${\displaystyle m}$ kütleli noktasal bir cisim ${\displaystyle r}$ uzaklığındaki bir eksen etrafında dönerse bu cismin eylemsizlik momenti ${\displaystyle mr^{2}}$ olarak tanımlanır. Eğer cisim çok sayıda parçacıktan oluşmuşsa her bir parçacığın ${\displaystyle mr^{2}}$ si toplanarak cismin eylemsizlik momenti bulunur. Yani cisim sonsuz küçüklükteki ${\displaystyle dm}$ kütlelerinden meydana geliyorsa bu cismin eylemsizlik momenti
${\displaystyle \int r^{2}dm}$ olur.
Örneğin ${\displaystyle L}$ boyundaki ${\displaystyle M}$ kütleli düz bir çubuğun kütle merkezinden geçen eksene göre eylemsizlik momenti şöyle hesaplanır:

1. ${\displaystyle dr}$ boyundaki küçük bir parçanın kütlesi ${\displaystyle dm}$ ise ${\displaystyle dm={\frac {Mdr}{L}}}$
2. Eksen çubuğun kütle merkezinden geçtiği için integralin sınırları -L/2 ve L/2 olur. Bulduğumuz ${\displaystyle dm}$ yi formülde yerine koyarsak ${\displaystyle \int \limits _{-L/2}^{L/2}r^{2}{\frac {Mdr}{L}}}$
3. ${\displaystyle M}$ ve ${\displaystyle L}$ sabit olduğundan integralin dışına çıkar, integrali çözersek

${\displaystyle {\frac {ML^{2}}{12}}}$ bulunur.

Paralel eksenler teoremi

Paralel eksenler teoremi, kütle merkezinden geçen eksene göre eylemsizlik momenti bilinen bir cismin bu eksenden ${\displaystyle d}$ uzaklıktaki eksene göre eylemsizlik momentini bulmaya yarar. Bu teoreme göre
${\displaystyle I=I_{km}+Md^{2}}$
Örneğin bir çubuğun ucuna göre eylemsizlik momenti paralel eksenler teoremi kullanılarak şu şekilde hesaplanır:
Çubuğun kütle merkezine göre eylemsizlik momenti ${\displaystyle {\frac {ML^{2}}{12}}}$, çubuğun ucu, merkezden ${\displaystyle L/2}$ uzaklıkta. Denklemde bunları yerine koyarsak
${\displaystyle I={\frac {ML^{2}}{12}}+M(L/2)^{2}={\frac {ML^{2}}{3}}}$
Bu sonuç bir çubuğu; merkezinin etrafında döndürmenin, ucunun etrafında döndürmeye göre daha kolay olduğunu gösterir.

Kütleyle olan benzerliği

Kütle, bir cismin öteleme hareketindeki eylemsizliğidir. Eylemsizlik momentiyse dönme hareketindeki eylemsizliktir. Bu ikisi arasındaki benzerlik hareket formüllerinde görülebilir.

	Öteleme hareketi	Dönme hareketi
Öteleme kinetik enerjisi ve dönme kinetik enerjisi	${\displaystyle E_{kin}={1 \over 2}mv^{2}}$	${\displaystyle E_{kin}={1 \over 2}I\omega ^{2}}$
Doğrusal momentum ve açısal momentum	${\displaystyle P=mv}$	${\displaystyle L=I\omega }$
Kuvvet ve tork	${\displaystyle F=ma}$	${\displaystyle \tau =I\alpha }$

• ${\displaystyle v}$: hız
• ${\displaystyle \omega }$: açısal hız
• ${\displaystyle m}$: kütle
• $a$: ivme
• ${\displaystyle \alpha }$: açısal ivme

Bâzı cisimlerin eylemsizlik momentleri

Aşağıdaki hesaplamalarda cisimlerin homojen oldukları kabul edilmiştir.

NOT: Dönme ekseni aksi belirtilmedikçe kütle merkezi olarak kabul edilecektir. I_x dönme eksenin x ekseni,I_y dönme eksenin y ekseni, I_z dönme eksenin z ekseni olduğunu gösterir.

Tanım	Şekil	Eylemsizlik Momenti	Açıklama
r yarıçaplı ve m kütleli ince silindir kabuk.		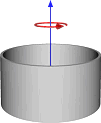${\displaystyle I=mr^{2}\,\!}$	Burada silindirin kalınlığı ihmal edilecek kadar küçüktür.
İçinde silindir şeklinde oyuk bulunan büyük bir silindir. İç yarıçapı r1 , dış yarıçapı r2, yüksekliği h ve kütlesi m.		${\displaystyle I_{z}={\frac {1}{2}}m\left({r_{1}}^{2}+{r_{2}}^{2}\right)}$ ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{2}}^{2}+{r_{1}}^{2}\right)+h^{2}\right]}$
r yarıçaplı, h yükseklikli ve m kütleli içi dolu silindir.		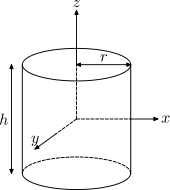${\displaystyle I_{z}={\frac {mr^{2}}{2}}\,\!}$ ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left(3r^{2}+h^{2}\right)}$	Bu bir önceki nesnenin r1=0 olduğu özel bir durumudur.
r yarıçaplı ve m kütleli ince, içi dolu disk.		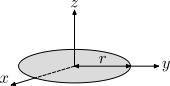${\displaystyle I_{z}={\frac {mr^{2}}{2}}\,\!}$ ${\displaystyle I_{x}=I_{y}={\frac {mr^{2}}{4}}\,\!}$	Bir önceki nesnenin h=0 için özel durumudur.
r yarıçaplı ve m kütleli çember.		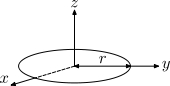${\displaystyle I_{z}=mr^{2}\!}$ ${\displaystyle I_{x}=I_{y}={\frac {mr^{2}}{2}}\,\!}$	Burada Iz dönme ekseninin z olduğunu gösterir.
r yarıçaplı ve m kütleli içi dolu küre.		${\displaystyle I={\frac {2mr^{2}}{5}}\,\!}$	Bir disk yarıçapı 0'dan r kadar değişen disklerin sonsuz ince disklerin birleşimi olarak kabul edilebilir.
r yarıçaplı m kütleli içi boş küre.		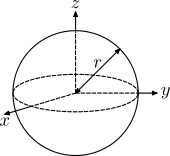${\displaystyle I={\frac {2mr^{2}}{3}}\,\!}$	Katı küreye benzer bir şekilde boş küre de çemberlerin birleşimi olarak düşünülebilir.
a dönme eksenli ve m kütleli, a, b, ve c yarı eksenli Elipsoid		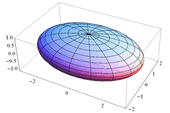${\displaystyle I_{a}={\frac {m(b^{2}+c^{2})}{5}}\,\!}$	—
r yarıçaplı, h yüksekli ve m kütleli dik koni		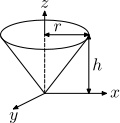${\displaystyle I_{z}={\frac {3}{10}}mr^{2}\,\!}$ ${\displaystyle I_{x}=I_{y}={\frac {3}{5}}m\left({\frac {r^{2}}{4}}+h^{2}\right)\,\!}$	—
Yüksekliği h, eni w, derinliği d, ve kütlesi m olan dikdörtgenler prizması.		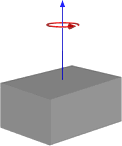${\displaystyle I_{h}={\frac {1}{12}}m\left(w^{2}+d^{2}\right)}$ ${\displaystyle I_{w}={\frac {1}{12}}m\left(h^{2}+d^{2}\right)}$ ${\displaystyle I_{d}={\frac {1}{12}}m\left(h^{2}+w^{2}\right)}$	${\displaystyle s}$ kenar uzunluklu küp için , ${\displaystyle I_{CM}={\frac {ms^{2}}{6}}\,\!}$ olur.
Yüksekliği D, genişliği W, uzunluğu L, ve kütlesi m olan içi dolu diktörtgenler prizması en uzun köşegen ekseninde döndürlürse.		${\displaystyle I={\frac {m\left(W^{2}D^{2}+L^{2}D^{2}+L^{2}W^{2}\right)}{6\left(L^{2}+W^{2}+D^{2}\right)}}}$	${\displaystyle s}$ kenarlı küp için, ${\displaystyle I={\frac {ms^{2}}{6}}\,\!}$.
İnce diktörtgen düzlem. h yüksekliği ,w genişliğ ve m kütlesi.		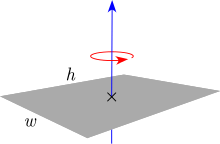${\displaystyle I_{c}={\frac {m(h^{2}+w^{2})}{12}}\,\!}$
İnce diktörtgen düzlem. h yüksekliği ,w genişliğ ve m kütlesi. (Dönme ekseni diktörtgenin ucunda)		${\displaystyle I_{e}={\frac {mh^{2}}{3}}+{\frac {mw^{2}}{12}}\,\!}$
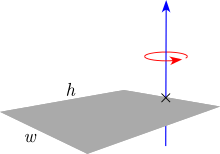L uzunluklu ve m kütleli ince çubuk.		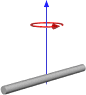${\displaystyle I_{\mathrm {center} }={\frac {mL^{2}}{12}}\,\!}$	Bu eşitlik çubuğun kalınlığının önemsiz olduğunu varsayar. Bu durum bir önceki nesnenin w = L veh = 0 olduğu özel bir durumudur.
L uzunluklu ve m kütleli ince çubuk. (Dönme ekseni çubuğun sonunda)		${\displaystyle I_{\mathrm {end} }={\frac {mL^{2}}{3}}\,\!}$	Bu eşitlik çubuğun kalınlığının önemsiz olduğunu varsayar. Bu da diktörtgenin h = L ve w = 0 olduğu özel bir durumudur.
İç yarıçapı a, kesit yarıçapı b ve kütlesi m olan Torus.		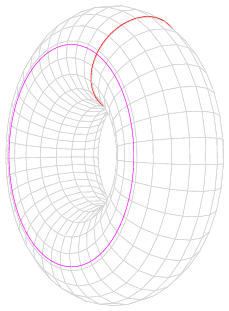Çap etrafında: ${\displaystyle {\frac {1}{8}}\left(4a^{2}+5b^{2}\right)m}$ Düşey eksen etrafında: ${\displaystyle \left(a^{2}+{\frac {3}{4}}b^{2}\right)m}$	—
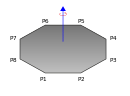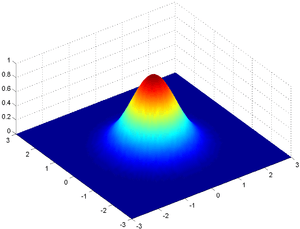
Poligon düzlemi.Kenarları ${\displaystyle {\vec {P}}_{1}}$, ${\displaystyle {\vec {P}}_{2}}$, ${\displaystyle {\vec {P}}_{3}}$, ..., ${\displaystyle {\vec {P}}_{N}}$ ve kütlesi ${\displaystyle m}$ iç kısımda homojen dağılımlı, düzleme dik ve merkez ekseninde dönmekte.		${\displaystyle I={\frac {m}{6}}{\frac {\sum \limits _{n=1}^{N-1}\|{\vec {P}}_{n+1}\times {\vec {P}}_{n}\|({\vec {P}}_{n+1}^{2}+{\vec {P}}_{n+1}\cdot {\vec {P}}_{n}+{\vec {P}}_{n}^{2})}{\sum \limits _{n=1}^{N-1}\|{\vec {P}}_{n+1}\times {\vec {P}}_{n}\|}}}$	—
Sonsuz disk. Kütlesi dönme ekseni etrafında normal dağılım göstermekte. (Örneğin: ${\displaystyle \rho (x,y)={\tfrac {m}{2\pi ab}}\,e^{-((x/a)^{2}+(y/b)^{2})/2}}$ Burada : ${\displaystyle \rho (x,y)}$ x ve y'nin fonksiyonu olarak kütle yoğunluğu'dur.).		${\displaystyle I=m(a^{2}+b^{2})\,\!}$
Aralarında x uzaklığı bulunan M ve m kütleli iki nokta.		${\displaystyle I={\frac {Mm}{M\!+\!m}}x^{2}=\mu x^{2}}$	${\displaystyle \mu }$ etkin kütle'i göstermektedir. ${\displaystyle \mu ={\cfrac {m_{1}m_{2}}{m_{1}+m_{2}}},\!\,}$

Kaynaklar