Karmaşık karesel polinom

Bir karmaşık karesel polinom bir karesel polinom böylece katsayılar karmaşık sayılardır.

Formlar

Eğer karesel polinomun yalnız tek değişkeni var ise (tek değişkenli),bu 4 ana formlara ayrılabilir:

• genel form: ${\displaystyle f(x)=a_{2}x^{2}+a_{1}x+a_{0}\qquad \,}$ burada ${\displaystyle \qquad a_{2}\neq 0}$
• Çarpanlı form mantık haritası için kullanılıyor ${\displaystyle f_{r}(x)=rx(1-x)\,}$
• ${\displaystyle f_{\theta }(x)=x^{2}+e^{2\pi \theta i}x\,}$ bunda orijinden kayıtsız sabitlenmiş nokta ile çarpıcı ${\displaystyle \lambda =e^{2\pi \theta i}\,}$ ^[1] var
• monik ve merkezi form, ${\displaystyle f_{c}(x)=x^{2}+c\,}$

monik ve merkezi formun aşağıdaki özellikleri var:

• Bu bir tek katsayı ile doğrusal olmayan fonksiyon'un basit formudur(parametre),
• Bu bir tekkritik polinomdur, yani, bunun tek kritik noktası var,
• Bu bir merkezi polinomdur ( kritik noktaların toplamı sıfırdır),^[2]
• Eğer kritik noktanın yörüngesi sonlu ise bu kritik-sonrası sonlu olabilir . Bu kritik nokta ise periyodik veya periyodik öncesidir.^[3]
• Bu bir tek-modlu fonksiyondur,
• Bu bir kesirli fonksiyondur,
• Bu bir tam fonksiyondur.

Eşlenik

Ara formlar

Öyleki ${\displaystyle f_{c}(x)\,}$ kuadratik polinomun genel formu için sıklıkla karmaşık dinamikler çalışması için afin eşlenik ve Mandelbrotun yaratılan imajı için kullanılıyor,Julia ve Fatou setleri.

Eğer ${\displaystyle \theta \,}$ dan ${\displaystyle c\,}$:^[4]

${\displaystyle c=c(\theta )={\frac {e^{2\pi \theta i}}{2}}\left(1-{\frac {e^{2\pi \theta i}}{2}}\right)}$.

Eğer ${\displaystyle r\,}$ den ${\displaystyle c\,}$ ye tek değişiklik isteniyorsa:^[5]

${\displaystyle c=c(r)\,=\,{\frac {1-(r-1)^{2}}{4}}}$.

Çift harita ile

Burada yarı-eşlenik diyadik dönüşüm arasında (burada ikili harita adıyla) ve kuadratik polinom.

Aile

${\displaystyle f_{c}:z\to z^{2}+c\,}$ kuadratik polinomların ailesi ${\displaystyle c\in \mathbb {C} \,}$ ile ölçeklendirilir ve adlandırılır:

• kuadratik polinomların Douady-Hubbard ailesi^[6]
• kuadratik aile

Harita

monik ve merkezi formun değişken ${\displaystyle z\,}$ ve ölçek $c\,$ ile kullanımı tipiktir:

${\displaystyle f_{c}(z)=z^{2}+c.\,}$

Eğer bu ayrık nonlineer dinamik sistemin bir evirme fonksiyonu olarak kullanılıyorsa:

${\displaystyle z_{n+1}=f_{c}(z_{n})\,}$

buna kuadratik harita denir :^[7]

${\displaystyle f_{c}:z\to z^{2}+c.\,}$

Bu Mandelbrot kümesi için ardışık yoldur.

Gösterim

Burada ${\displaystyle f^{n}\,}$ fonksiyon ${\displaystyle f\,}$ in n-inci ardışık ifadesi ve üstel değil

${\displaystyle f_{c}^{n}(z)=f_{c}^{1}(f_{c}^{n-1}(z))\,}$

böylece

${\displaystyle z_{n}=f_{c}^{n}(z_{0}).\,}$

olası bir karışıklık için bu ${\displaystyle f.\,}$ fonksiyonunun ardışık n.inci ifadesi için ${\displaystyle f^{\circ n}\,}$ alışılmış şekliyle yazılır

Kritik öğeler

Kritik nokta

${\displaystyle f_{c}\,}$ ${\displaystyle z_{cr}\,}$ in bir kritik noktası ve dinamik düzlemde böylece türev kaybolur:

${\displaystyle f_{c}'(z_{cr})=0.\,}$

ile

${\displaystyle f_{c}'(z)={\frac {d}{dz}}f_{c}(z)=2z}$

vurgusu

${\displaystyle z_{cr}=0\,}$

Bizim bu ${\displaystyle f_{c}\,}$ nin yalnız (sonlu) kritik nokta gördüğümüz noktası ${\displaystyle z_{cr}=0\,}$ dır.

${\displaystyle z_{0}}$ Mandelbrot kümesi ardışıği için bir başlangıç noktasıdır.^[8]

Kritik değer

${\displaystyle f_{c}\,}$ nin ${\displaystyle z_{cv}\ }$ bir kritik değeri bir kritik noktanın görüntüsüdür:

${\displaystyle z_{cv}=f_{c}(z_{cr})\,}$

ile

${\displaystyle z_{cr}=0\,}$

elimizde olan

${\displaystyle z_{cv}=c.\,}$

Böylece ${\displaystyle c\,}$ ölçeği ${\displaystyle f_{c}(z).\,}$ nin kritik değeridir

Kritik yörünge

Dinamik düzlem ile kritik yörünge 3-periyod döngü içine düşüyor

Dinamik düzlem ile Julia seti ve kritik yörünge.

Dynamical plane : changes of critical orbit along internal ray of main cardioid for açı 1/6

Critical orbit tending to weakly attracting fixed point with abs(multiplier)=0.99993612384259

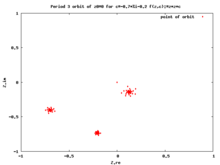
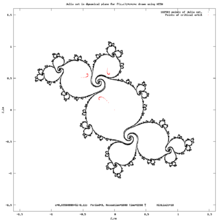
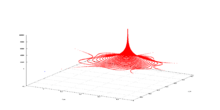
Bir kritik noktanın ileri yörünge bir kritik yörüngesi denir.Kritik yörüngeler çok önemli çünkü her periyodik yörüngebir kritik nokta çekiyor böylece Fatou seti.^[9][10] içindeki dinamikleri anlamaya yardımcı kritik yörüngeler açıklanmıştır.

${\displaystyle z_{0}=z_{cr}=0\,}$

${\displaystyle z_{1}=f_{c}(z_{0})=c\,}$

${\displaystyle z_{2}=f_{c}(z_{1})=c^{2}+c\,}$

${\displaystyle z_{3}=f_{c}(z_{2})=(c^{2}+c)^{2}+c\,}$

${\displaystyle ...\,}$

Bu yörünge bir çekimsel periyodik döngü içine düşüyor.

Kritik kesit

kritik kesit dinamik düzlemin bir kesitidir ve kritik nokta içeriyor.

Kritik polinom

${\displaystyle P_{n}(c)=f_{c}^{n}(z_{cr})=f_{c}^{n}(0)\,}$

böylece

${\displaystyle P_{0}(c)=0\,}$

${\displaystyle P_{1}(c)=c\,}$

${\displaystyle P_{2}(c)=c^{2}+c\,}$

${\displaystyle P_{3}(c)=(c^{2}+c)^{2}+c\,}$

kullanılan bu polinomlar :

• n periyodlu bu Mandelbrot set bileşenlerinin bulunduğu merkezlerdir. Merkezler n-inci kritik polinomun kökleridir

${\displaystyle centers=\{c:P_{n}(c)=0\}\,}$

• n periyodun Mandelbrot set bileşenlerinin kökleri bulunuyor (${\displaystyle P_{n}(c)\,}$ nin yerel minimumu)
• Misiurewicz noktaları

${\displaystyle M_{n,k}=\{c:P_{k}(c)=P_{k+n}(c)\}\,}$

Kritik eğriler

Kritik polinomların diyagramına kritik eğriler denir.^[11]

Bu eğriler dallanma diyagramının iskeletini yaratırlar .^[12] (siyah çizgiler^[13])

Düzlemler

w-düzlem ve c-düzlem

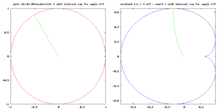
Bu dinamik sistemin bir global analizi için 4-boyutlu uzay Julia-Mandelbrot kullanılabilir .^[14]

bu uzay içinde burada 2-D düzlemlerin 2 temel tipi :

• dinamik (dinamik) düzlem, ${\displaystyle f_{c}\,}$-düzlem veya c-düzlem
• parametre düzlemi veya z-düzlemi

Burada ayrıca diğer düzlem gibi dinamik sistemlerin analizi için w-düzlemi kullanılıyor:

• eşlenik düzlem^[15]
• model düzlem^[16]

Parametre düzlemler

Karmaşık mantıksal harita için Gamma parametre düzlemi${\displaystyle z_{n+1}=\gamma z_{n}\left(1-z_{n}\right),}$

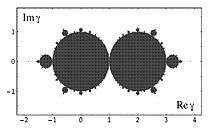
Bir kuadratik haritanın faz uzayına parametre düzlem denir. Burada:

${\displaystyle z0=z_{cr}\,}$ sabit ve $c\,$ değikendir.

Bu dinamikler burada yoktur.Bu parametre değerlerin yalnız bir kümesidir. Burada parametre düzlem üzerinde yörüngeler yoktur.

• Mandelbrot set
  • bifurkasyon lokusu =Mandelbrot setinin sınırları
  • Mandelbrot kümesinin hiperbolik bileşenlerinin sınırları= Mandelbrot setinin içinin oluşturduğu parametre düzlem^[17]

Buradaki parametre düzlemin birçok farklı alttipidir.^[18][19]

Dinamik düzlem

bir dinamik düzlem üzerinde bulunabilenler:

• Julia seti
• Filled Julia seti
• Fatou seti
• Yörüngeler

ve

• Fatou set
• Julia set

lerinin oluşturduğu dinamik düzlem.Burada, $c\,$ bir sabit ve ${\displaystyle z\,}$ bir değişkendir.

iki-boyutlu dinamik düzlem sürekli dinamik sistemin üç-boyutlu uzayının bir Poincaré çapraz-bölümü olarak davranabilir .^[20][21]

Türevler

c ye göre türev

parametre düzlem üzerinde:

• ${\displaystyle c}$ bir değişkendir
• ${\displaystyle z_{0}=0}$ sabittir

c ye göre türev ${\displaystyle f_{c}^{n}(z_{0})}$'in ilk türevidir

${\displaystyle z_{n}'={\frac {d}{dc}}f_{c}^{n}(z_{0}).}$

Bu türev ardışıklık ile başlatılabilir

${\displaystyle z_{0}'={\frac {d}{dc}}f_{c}^{0}(z_{0})=1}$

ile başlar ve her ardışık adımda yerine konulursa

${\displaystyle z_{n+1}'={\frac {d}{dc}}f_{c}^{n+1}(z_{0})=2\cdot {}f_{c}^{n}(z)\cdot {\frac {d}{dc}}f_{c}^{n}(z_{0})+1=2\cdot z_{n}\cdot z_{n}'+1.}$

Bu türev için zincir kuralı kullanılarak kolayca doğrulanabilir .

Bu türev Bir Mandelbrot kümesi çizimi için uzaklık tahmin yöntemi içinde kullanılıyor.

z ye göre türev

Dinamik düzlem üzerinde:

• ${\displaystyle z}$ bir değişken
• ${\displaystyle c}$ bir sabittir

bir sabitlenmiş nokta ${\displaystyle z_{0}\,}$ da

${\displaystyle f_{c}'(z_{0})={\frac {d}{dz}}f_{c}(z_{0})=2z_{0}}$

periyod p nin bir z₀ periyodik noktasında

${\displaystyle (f_{c}^{p})'(z_{0})={\frac {d}{dz}}f_{c}^{p}(z_{0})=\prod _{i=0}^{p-1}f_{c}'(z_{i})=2^{p}\prod _{i=0}^{p-1}z_{i}.}$

Bu periyodik (ayrıca sabitlenmiş) noktaların kararlılığını doğrulamak için kullanılıyor.

periyodik olmayan noktada:

${\displaystyle z'_{n}\,}$

Bu türev ardışıklık ile bulunabilir,başlaması

${\displaystyle z'_{0}=1\,}$

iledir ve sonra:

${\displaystyle z'_{n}=2*z_{n-1}*z'_{n-1}\,}$

Bu türev Julia seti için dış uzunluk hesaplamada kullanılıyor.

Schwarzian türev

f nin Schwarzian türevi ( kısacası SD):^[22]

${\displaystyle (Sf)(z)={\frac {f'''(z)}{f'(z)}}-{\frac {3}{2}}\left({\frac {f''(z)}{f'(z)}}\right)^{2}}$.

Ayrıca bakınız

• Misiurewicz noktası
• Karmaşık karesel haritalamanın periyodik noktaları
• Mandelbrot kümesi
• Julia seti
• Milnor-Thurston yoğurma kuramı

Kaynakça

1. Michael Yampolsky, Saeed Zakeri : Mating Siegel quadratic polynomials.
2. B Branner: Holomorphic dynamical systems in the complex plane. Mat-Report No 1996-42. Technical University of Denmark
3. Alfredo Poirier : On Post Critically Finite Polynomials Part One: Critical Portraits
4. ya tek değişiklik istiyor Michael Yampolsky, Saeed Zakeri : Mating Siegel quadratic polynomials.
5. stackexchange questions : Show that the familiar logistic map ...
6. Yunping Jing : Local connectivity of the Mandelbrot set at certain infinitely renormalizable points Complex Dynamics and Related Topics, New Studies in Advanced Mathematics, 2004, The International Press, 236-264
7. Weisstein, Eric W. "Quadratic Map." From MathWorld--A Wolfram Web Resourc
8. Java program by Dieter Röß showing result of changing initial point of Mandelbrot iterations
9. M. Romera, G. Pastor, and F. Montoya : Multifurcations in nonhyperbolic fixed points of the Mandelbrot map. Fractalia 6, No. 21, 10-12 (1997)
10. Burns A M : Plotting the Escape: An Animation of Parabolic Bifurcations in the Mandelbrot Set. Mathematics Magazine, Vol. 75, No. 2 (Apr., 2002), pp. 104-116
11. The Road to Chaos is Filled with Polynomial Curves by Richard D. Neidinger and R. John Annen III. American Mathematical Monthly, Vol. 103, No. 8, October 1996, pp. 640-653
12. Hao, Bailin (1989). Elementary Symbolic Dynamics and Chaos in Dissipative Systems. World Scientific. ISBN 9971-5-0682-3. http://power.itp.ac.cn/~hao/. 
13. M. Romera, G. Pastor and F. Montoya, "Misiurewicz points in one-dimensional quadratic maps", Physica A, 232 (1996), 517-535. Preprint
14. Julia-Mandelbrot Space at Mu-ency by Robert Munafo
15. Carleson, Lennart, Gamelin, Theodore W.: Complex Dynamics Series: Universitext, Subseries: Universitext: Tracts in Mathematics, 1st ed. 1993. Corr. 2nd printing, 1996, IX, 192 p. 28 illus., ISBN 978-0-387-97942-7
16. Holomorphic motions and puzzels by P Roesch
17. Lasse Rempe, Dierk Schleicher : Bifurcation Loci of Exponential Maps and Quadratic Polynomials: Local Connectivity, Triviality of Fibers, and Density of Hyperbolicity
18. Alternate Parameter Planes by David E. Joyce
19. exponentialmap by Robert Munafo
20. Mandelbrot set by Saratov group of theoretical nonlinear dynamics
21. Moehlis, Kresimir Josic, Eric T. Shea-Brown (2006) Periodic orbit. Scholarpedia,
22. The Schwarzian Derivative & the Critical Orbit by Wes McKinney ­ 18.091 ­ 20 April 2005

Dış bağlantılar

• M. Nevins and D. Rogers, "Quadratic maps as dynamical systems on the p-adic numbers"
• Wolf Jung : Homeomorphisms on Edges of the Mandelbrot Set. Ph.D. thesis of 2002

Şablon:Chaos theory