İkizkenar üçgen

İki kenarı birbirine eşit olan çokgenlerdir. İç açıları toplamı 180°'dir.

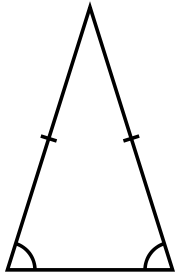
İkizkenar üçgen

Özellikleri

• İkizkenar üçgende ikizkenarlara ait yükseklikler, açıortaylar, kenarortaylar ve kenar orta dikmeler eşittir.
• İkizkenar üçgende üçüncü kenar üzerindeki herhangi bir noktadan ikizkenarlara inilen dikmelerin toplam uzunluğu , eş kenarlara köşelerden inilen yüksekliklerin uzunluğuna eşittir.
• İkizkenar üçgende üçüncü kenar üzerindeki herhangi bir noktadan ikizkenarlara çizilen paralellerin toplam uzunluğu ikizkenarların uzunluğuna eşittir.
• Üçüncü kenara ait yükseklik; açıortay, kenarortay ve kenar orta dikmedir.
• İkizkenar üçgenlerde tepe açısının açıortayı aynı zamanda kenarortay ve yüksekliktir.

İkizkenar üçgende kosinüs teoremi

Bir ikizkenar üçgende ${\displaystyle a=b}$ ve iki eşit kenar arasındaki açı ${\displaystyle \gamma }$ olduğu durumda ${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma }$ olan kosinüs teoremi aşağıdaki şekli alır:

${\displaystyle \cos(\gamma )=1-{\frac {c^{2}}{2a^{2}}}.\;}$