F-dağılımı

Fisher-Snedecor

Olasılık yoğunluk fonksiyonu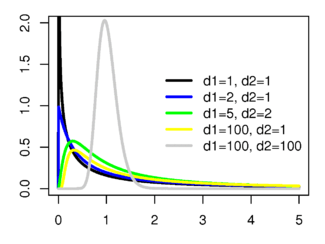
Yığmalı dağılım fonksiyonu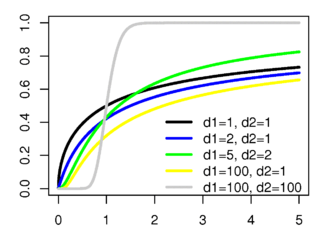
Parametreler	${\displaystyle d_{1}>0,\ d_{2}>0}$ serbestlik derecesi
Destek	${\displaystyle x\in [0;+\infty )\!}$
Olasılık yoğunluk fonksiyonu (OYF)	${\displaystyle {\frac {\sqrt {\frac {(d_{1}\,x)^{d_{1}}\,\,d_{2}^{d_{2}}}{(d_{1}\,x+d_{2})^{d_{1}+d_{2}}}}}{x\,\mathrm {B} \!\left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\!}$
Yığmalı dağılım fonksiyonu (YDF)	${\displaystyle I_{\frac {d_{1}x}{d_{1}x+d_{2}}}(d_{1}/2,d_{2}/2)\!}$
Ortalama	${\displaystyle {\frac {d_{2}}{d_{2}-2}}\!}$ eger ${\displaystyle d_{2}>2}$
Medyan
Mod	${\displaystyle {\frac {d_{1}-2}{d_{1}}}\;{\frac {d_{2}}{d_{2}+2}}\!}$ eger ${\displaystyle d_{1}>2}$
Varyans	${\displaystyle {\frac {2\,d_{2}^{2}\,(d_{1}+d_{2}-2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)}}\!}$ eger ${\displaystyle d_{2}>4}$
Çarpıklık	${\displaystyle {\frac {(2d_{1}+d_{2}-2){\sqrt {8(d_{2}-4)}}}{(d_{2}-6){\sqrt {d_{1}(d_{1}+d_{2}-2)}}}}\!}$ burada ${\displaystyle d_{2}>6}$
Fazladan basıklık	Metine bakın
Entropi
Moment üreten fonksiyon (mf)	Momentler icin metine bakın
Karakteristik fonksiyon

Olasılık kuramı ve istatistik bilim kollarında, F-dağılımı bir sürekli olasılık dağılımdır. Bu dağılımı ilk bulan istatistikçiler olan R.A. Fisher veGeorge W. Snedecor adlarına bağlı olarak Snedecor'un F dağılımı veya Fisher-Snedecor dağılımı olarak da anılmaktadir.

F-dagılımı için rassal değişir, iki ki-kare dağılım gösteren değişirin oranı olarak ortaya çıkar:

${\displaystyle {\frac {U_{1}/d_{1}}{U_{2}/d_{2}}}}$

burada

• U₁ ve U₂ aynı sırayla d₁ ve d₂ serbestlik derecesi gösteren ki-kare dağılımları ve
• U₁ ve U₂ bağımsızdırlar (Bir uygulama için Cochran'in teoremine bakın).

Böylelikle F-dağılımı. d₁ birinci veya alt serbestlik derecesi ve d₂, ikinci veya üst serbestlik derecesi parametreleri ile tam olarak tanımlanır.

F-dağılımı çok sık olarak bir test istatistiğinin sıfır hipotezi olarak pratikte kullanılır. Bu pratik kullanış en çok tanınmış şekilde, çok zaman F-testi olarak anılarak, varyanslar analizindedir. Daha az tanınmış kullanış alanları ise olunabilirlilik-oranı testlerindedir.

F-dağılımı için beklenen değer, varyans ve çarpıklık katsayısı için formüüller yukarıdaki bilgi-kutusunda verilmiştir. İkinci serbestlik derecesi ${\displaystyle d_{2}>8}$ ise basıklık katsayısı şöyle ifade edilir:

${\displaystyle {\frac {12(20d_{2}-8d_{2}^{2}+d_{2}^{3}+44d_{1}-32d_{1}d_{2}+5d_{2}^{2}d_{1}-22d_{1}^{2}+5d_{2}d_{1}^{2}-16)}{d_{1}(d_{2}-6)(d_{2}-8)(d_{1}+d_{2}-2)}}.}$

F(d₁, d₂) ifadesi ile açıklanan F-dağılımı gösteren bir rassal değişken için olasılık yoğunluk fonksiyonu şöyledir:

${\displaystyle g(x)={\frac {1}{\mathrm {B} (d_{1}/2,d_{2}/2)}}\;\left({\frac {d_{1}\,x}{d_{1}\,x+d_{2}}}\right)^{d_{1}/2}\;\left(1-{\frac {d_{1}\,x}{d_{1}\,x+d_{2}}}\right)^{d_{2}/2}\;x^{-1}}$

Burada x ≥ 0 bir reel; d₁ ve d₂ serbestlik dereceleri adı ile anılan pozitif tamsayılar; ve B bir beta fonksiyonu olur.

Yığmalı dağılım fonksiyonu şöyle ifade edilir:

${\displaystyle G(x)=I_{\frac {d_{1}x}{d_{1}x+d_{2}}}(d_{1}/2,d_{2}/2)}$

Burada I tanzim edilmiş tamam olmayan beta fonksiyonu olur.

Genelleştirme

(Merkezsel) F-dağılımının bir genelleştirilmesi merkezsel olmayan F-dağılımıdır.

İlişkili dağılımlar ve özellikler

• Eğer ${\displaystyle X\sim \mathrm {F} (\nu _{1},\nu _{2})}$ o zaman ${\displaystyle Y=\lim _{\nu _{2}\to \infty }\nu _{1}X}$ ${\displaystyle \chi _{\nu _{1}}^{2}}$ ifade edilen bir ki-kare dağılımı gosterir.
• ${\displaystyle F(\nu _{1},\nu _{2})}$ ölçeği değiştirilmiş Hotelling'in T-kare dağılımı ile, yani ${\displaystyle (\nu _{1}(\nu _{1}+\nu _{2}-1)/\nu _{2})T^{2}(\nu _{1},\nu _{1}+\nu _{2}-1)}$ ile tıpatıp aynıdır.
• F-dağılımının ilgi çeken bir özelliği, ${\displaystyle X\sim F(\nu _{1},\nu _{2})}$ ise ${\displaystyle {\frac {1}{X}}\sim F(\nu _{2},\nu _{1})}$ olmasıdır.

Dışsal bağlantılar

• F-dağılımı için kritik değerler tablosu.
• F-dağılımı kullarak online hipotez sınama.
• Dağılım hesaplayıcısı: Normal dağılım, t-dağılımı, ki-kare-dağılımı and F-dağılımı için olasılıklar ve kritik değerler hesaplayıcısı
• Fisher'in F-dağılımı için yığmalı olasılık fonksiyonu hesaplayıcısı.
• Fisher'in F-dağılımı için olasılık yoğunluk fonksiyonu hesaplayıcisı.