Vektörlerin eşdeğişken ve karşıtdeğişkeni

"Eşdeğişkin" veya "karşıtdeğişkin"in diğer kullanıcıları için, bkz eşdeğişkin ve karşıtdeğişkin (anlam ayrımı).

Bir vektör v (kırmızı) ile gösteriliyor • Vektörlerin tanjant tabanı koordinat eğrilerine (siyah) (sarı, sol: e₁, e₂, e₃), • ikili taban, eşvektör taban, veya eştaban (mavi,sağ: e¹, e², e³), yüzey koordinatlarına normal vektörler (gri), 3d içinde genel eğrisel koordinatlar (q¹, q², q³)...Bir pozisyon uzayının içinde tanımlanan noktalara sayıların bir demeti denir. Unutmadan taban ve eştaban uyuşmuyorsa tabanı olmadıkça ortogonaldir.^[1]

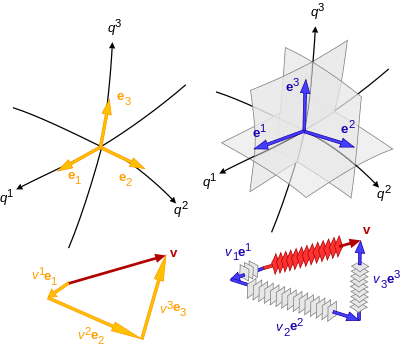
Çokludoğrusal cebir ve tensör analizi içinde, eşdeğişkin ve karşıtdeğişkin veya tabanın değişimi ile bir fiziksel veya geometrisi belli nesnenin değişikliğinin nicel tanımlaması nasıl yapılır?

Holonomik taban için, bu bir koordinat sisteminden diğerine değişme ile belirlenir: Eğer bir ortogonal taban diğer ortogonal tabanin içinde döner ise,eş- ve karşıtdeğişkin ayrımı görünmezdir. Bununla birlikte,daha genel koordinat sistemleri ve böylece çarpık koordinatlar gözönüne alındığında , eğrisel koordinatlar ve diferansiyellenebilir manifoldlar üzerinde koordinat sistemlerinde ayrımi belirgindir(görünürdür).

• Bir vektör için (bir yön vektörü veya hız vektörü gibi) taban-bağımsız ,vektör bileşenlerini dengelemek için tabanın bir değişikliği ile karşıt-değişebilir olmalıdir. Diğer bir deyişle, bileşenler esas değişiminin bu ters dönüşüm ile değişmesi gerekir.Vektör bileşenlerinin (ikili vektörlerin olanlara karşıt olarak) karşıtdeğişkin olduğu söyleniyor. Örneğin vektörler l karşıtdeğişkin bileşenler ile bir gözlemciye göre bir nesnenin konumunu içerir,veya zamana göre sırasıyla konumun herhangi türevi,hız, ivme,ve jerk içerir.Einstein gösteriminde karşıtdeğişkin bileşenler üst indisleri ile gösterilir

${\displaystyle \mathbf {v} =v^{i}\mathbf {e} _{i}.}$ içinde üst indis olarak ifade edilir

• Taban-bağımsız olan (aynı zamanda bir eşvektör olarak da adlandırılır), bir ikili vektörü için, ikili vektörün bileşenlerinin aynı eşvektörü gösterir kalması için tabandaki bir değişiklik ile birlikte eş-değişebilir olması gerekir.

Diğer bir deyişle, bileşenler esas değişikliği ile aynı dönüşüme göre farklılık gerekir. Ikili vektörler (vektörlerin kişilerce aksine) bileşenlerinin eşdeğişkin olduğu söylenmektedir.Örneğin eşdeğişirin örnek vektörleri genel olarak görünür bir fonksiyonun bir gradyanı alınır ise Einstein gösterimi içinde, eşdeğişkin bileşenler

${\displaystyle \mathbf {v} =v_{i}\mathbf {e} ^{i}.}$ içinde alt indis olarak ifade edilir

Fizikte, sıklıkla vektörlerin uzunluk birimi veya zaman uzunluğu bazı diğer birimler (hız gibi) var, oysa eşvektörlerin uzunluğun tersi birimleri veya zaman uzunluğunun tersi bazı diğer birimler var.Eşdeğişkin ve karşıtdeğişkin ve vektörleri arasındaki ayrım karışık varyansa sahip olabilir ki, tensör hesaplamaları için özellikle önemlidir. Bu da hem eşdeğişkin ve hem karşıtdeğişkin bileşeni var demektir.Değerlik veya tipi bir tensör eşdeğişken ve karşıtdeğişkin ve bileşen indislerinin sayısını verir.

Eşdeğişir ve zıtdeğişir terimleri J.J. Sylvester tarafından 1853 yılı içinde cebrik değişmezlik teorisinin incelenmesi amacıyla tanıtıldı. Bu kavramlar içinde, örneğin,eşzamanlı denklemler sistem değişkenleri içinde zıtdeğişirdir. Kullanılan her iki terim çoklu-doğrusal cebirin kategori teorisi içinde modern kavramlarını karşılayan özel bir örnektir.

Tanıtım

Fizikte,tipik bir vektör bir ölçümün çıkışı veya ölçümlerin serisi olarak ortaya çıkar, ve sayıların gösterim olarak bir listesi (veya demet) gibidir

${\displaystyle (v_{1},v_{2},v_{3}).\,}$

Listedeki sayılar koordinat sisteminin seçimine örneğin, eğer sırasıyla vektör gösterimlerinin pozisyonu bir gözlemciye (pozisyon vektörü)bağlı, ise koordinat sistemi katı çubukların bir sisteminden elde edilebilir, veya referans eksenleri, bu v₁, v₂ bileşenleri boyunca, ve v₃ ölçülmüştür. geometrik bir nesne gösteriminin bir vektörü için, herhangi diğer koordinat sistemleri içinde nasıl göründüğünü açıklamak mümkün olmalı. Demek ki,vektörlerin bileşenleri bir başka koordinat sistemine geçen belirli bir yol içinde dönüşüm olacak. Bir zıt-değişir vektör bu "koordinatlar olarak aynı yolla dönüşüm" (Referans eksenleri ters olacak şekilde) bileşenleri dönüş ve genişleme gibi koordinatların değişimi altında olması gerekir. bu işlemler altında değişmeyen vektörün kendisidir; bunun yerine,aynı şekilde bu koordinatların değişimi vektörün bileşenlerinin eksenel değişikliğini iptal eder bir değişiklik yapar. Başka bir değişle, Referans eksenleri bir yöne döndürülmesi durumunda, vektörünün bileşen temsilini tam tersi şekilde döndürmek istiyorum. Benzer şekilde, eğer referans eksenleri bir yöne çekildi,vektörün bileşenleri koordinatlar gibi bir tam dengeleyici bir şekilde düşürülebilecek.Matematiksel olarak, koordinat sistemi bir tersinir matris M tarafından tanımlanan bir dönüşüme uğrar ise , böylece bir koordinat vektör x , x′ = Mx a dönüşüyor,ise bir v karşıtdeğişken vektör v′ = Mv yoluyla benzer dönüşüm olmalı. Bu önemli gerek fiziksel nicel anlamlılığın herhangi diğer üçlüden bir karşıtdeğişinti vektörünü ayırır. Örneğin, Eğer v -hızın-x, y, ve z bileşenlerinin oluşturduğu,v bir karşıtdeğişken vektör ise: Eğer uzayın koordinatları aynı yol içinde hız dönüşümünün bileşenleri ise germe, dönme, veya bükülmedir.Diğe bir değişle, örneğin, bir dörtgen kutunun uzunluk, genişlik, ve yüksekliğin oluşturduğu bir üçlü bir soyut bir vektörün üç bileşenleri makyajlanabilir, ama bu vektör karşıtdeğişken olmayacak,kutu dönmesi nedeniyle kutunun uzunluk, genişlik, ve yüksekliği değişmiyor.Vektörlerin eşdeğişir örnekleri yerdeğiştirme, hız ve ivme içerir.

Buna karşılık, bir eşdeğişir vektör koordinatlara karşıt değiştirilebilir bileşenler veya, eşdeğerlikli,dönüşüm gibi referans eksenleri var.Örneğin, bir fonksiyonun gradyan vektörünün bileşenleri

${\displaystyle \nabla f={\frac {\partial f}{\partial x^{1}}}{\widehat {x}}^{1}+{\frac {\partial f}{\partial x^{2}}}{\widehat {x}}^{2}+{\frac {\partial f}{\partial x^{3}}}{\widehat {x}}^{3}}$

kendilerinin referans eksenleri dönüşümü gibi.Eksenlerin dönmeleri dikkate alındığında, karşıtdeğişintinin bileşenleri ve eşdeğişinti vektörler aynı yol içinde davranır.yalnız diğer dönüşümler bu ise bu farklı görüntü ayırıyoralır.

Tanım

tabanın değişimi altında bir koordinat vektör gibi dönüşümünün bileşenleri (pasif dönüşüm) eşdeğişir ve zıtdeğişirin genel formüllerine kaynaktır. Böylece diyelimki V S skalerinin bir alanı üzerinde n boyutunun bir vektör uzayı olsun , ve diyelimki f  = nin her (X₁,...,X_n) ve Vnin bir taban f' = (Y₁,...,Y_n) olsun.^{[note 1]} Ayrıca, diyelimki f dan f′ ye taban değişimi ile veriliyor olsun

${\displaystyle \mathbf {f} \mapsto \mathbf {f} '=\left(\sum _{i}a_{1}^{i}X_{i},\dots ,\sum _{i}a_{n}^{i}X_{i}\right)=\mathbf {f} A}$

bazı tersinir için n×n matris A ile giriş ${\displaystyle a_{j}^{i}}$. Burada, f' tabanın Y_j vektörü f tabanının 'Xi vektörlerinin bir doğrusal kombinasyonudur, böylece

${\displaystyle Y_{j}=\sum _{i}a_{j}^{i}X_{i}.}$

Karşıt değişken dönüşüm

V içindeki bir v vektörü f tabanının bir ögesinin bir doğrusal bileşiminin eşsiz bir ifadesi olarak

${\displaystyle v=\sum _{i}v^{i}[\mathbf {f} ]X_{i},}$

burada v ⁱ[f] ,S içinde skalerler , f tabanı içinde vnin

'bileşenleri olarak biliniyor.v[f] ile v bileşeninin sütun vektörü olarak ifade ediliyor:

${\displaystyle \mathbf {v} [\mathbf {f} ]={\begin{bmatrix}v^{1}[\mathbf {f} ]\\v^{2}[\mathbf {f} ]\\\vdots \\v^{n}[\mathbf {f} ]\end{bmatrix}}}$

böylece bir matris çarpımı olarak yeniden yazılabilir

${\displaystyle v=\mathbf {f} \,\mathbf {v} [\mathbf {f} ].}$

v vektörü f' tabanının terimleri içinde ayrıca ifade edilebilir, böylece

${\displaystyle v=\mathbf {f'} \,\mathbf {v} [\mathbf {f'} ].}$

Bununla birlikte, v vektörünün kendisi tabanın seçimi altında değişmezdir,

${\displaystyle \mathbf {f} \,\mathbf {v} [\mathbf {f} ]=v=\mathbf {f'} \,\mathbf {v} [\mathbf {f'} ].}$

vnin değişirliği ile f arasında ilişkililiği ile kombine edilir ve f' şunu anlatır

${\displaystyle \mathbf {f} \,\mathbf {v} [\mathbf {f} ]=\mathbf {f} A\,\mathbf {v} [\mathbf {f} A],}$

dönüşüm kural vererek

${\displaystyle \mathbf {v} [\mathbf {f} A]=A^{-1}\mathbf {v} [\mathbf {f} ].}$

Bileşenlerin terimleri içinde,

${\displaystyle v^{i}[\mathbf {f} A]=\sum _{j}{\tilde {a}}_{j}^{i}v^{j}[\mathbf {f} ]}$

burada katsayılar ${\displaystyle {\tilde {a}}_{j}^{i}}$ Anın ters matrisinin girişidir .

Çünkü A matrisinin tersi ile vektör v dönüşümünün bileşenleri, bu bileşenlere dönüşüm karşıt-değişkenliği altında bir tabanın değişikliği denir.

İki çiftin A yolu ilişkisi bir ok kullanarak aşağıda şemada resmi olmayan gösterimdir.Okun tersi bir karşıtdeğişken değişiklik gösterir:

${\displaystyle \mathbf {f} \longrightarrow \mathbf {f'} }$

${\displaystyle v[\mathbf {f} ]\longleftarrow v[\mathbf {f'} ]}$

Eşdeğişkin dönüşüm

V üzerinde bir α doğrusal fonksiyonel onun terimleri içinde eşsiz ifadesi (Siçinde skalerler) f tabanı içinde bileşenler dir

${\displaystyle \alpha (X_{i})=\alpha _{i}[\mathbf {f} ],\quad i=1,2,\dots ,n.}$ olarak

Bu bileşenler taban vektörleri X_i üzerinde α'nın hareketi f tabanındadır.

f den f' ye taban değişikliği altında, bileşenlerin dönüşümü böylece

${\displaystyle {\begin{array}{rcl}\alpha _{i}[\mathbf {f} A]&=&\alpha (Y_{i})\\&=&\alpha \left(\sum _{j}a_{i}^{j}X_{j}\right)\\&=&\sum _{j}a_{i}^{j}\alpha (X_{j})\\&=&\sum _{j}a_{i}^{j}\alpha _{j}[\mathbf {f} ]\end{array}}.}$

α[f] ile α'nın bileşenlerinin satır vektörü ifade edilir:

${\displaystyle \mathbf {\alpha } [\mathbf {f} ]={\begin{bmatrix}\alpha _{1}[\mathbf {f} ],\alpha _{2}[\mathbf {f} ],\dots ,\alpha _{n}[\mathbf {f} ]\end{bmatrix}}}$

böylece matris çarpımı olarak yeniden yazılabilir

${\displaystyle \alpha [\mathbf {f} A]=\alpha [\mathbf {f} ]A.}$

Çünkü doğrusal fonksiyonelin bileşenlerinin matris A ile α dönüşümü, bu bileşenler tabanın bir değişikliği altında dönüşüm eşdeğişirliği idi.

A yolu ilişkili iki çifti aşağıdakinin içindekine rağmen resmi olmayan bir diyagram oku kullanılıyor. Bir eşdeğişinti ilişkililiği belirtilmesi nedeniyle aynı yön içinde seyahat okudur:

${\displaystyle \mathbf {f} \longrightarrow \mathbf {f'} }$

${\displaystyle \alpha [\mathbf {f} ]\longrightarrow \alpha [\mathbf {f'} ]}$

Bir sütun vektör gösterimi yerine kullanılmıştı,dönüşüm kanunu devrik olmuş olsun

${\displaystyle \alpha ^{\mathrm {T} }[\mathbf {f} A]=A^{\mathrm {T} }\alpha ^{\mathrm {T} }[\mathbf {f} ].}$

Koordinatlar

V vektör uzayı üzerinde f tabanının seçilmesi V üzerinde koordinat fonksiyonlarının eşsiz bir kümesini tanımlar

${\displaystyle x^{i}[\mathbf {f} ](v)=v^{i}[\mathbf {f} ].}$'un

anlamı ile Koordinatlar V üzerinde bunun için karşıtdeğişken duyarlılık içinde bu

${\displaystyle x^{i}[\mathbf {f} A]=\sum _{k=1}^{n}{\tilde {a}}_{k}^{i}x^{k}[\mathbf {f} ].}$

Tersine,n çokluğunun bir sistemi vⁱ bu xⁱ gibi dönüşüm koordinatları V üzerinde bir karşıtdeğişkin vektör tanımlanıyor.Bir n sisteminin koordinatlara karşıt nicel dönüşümü o zaman bir eşdeğişkin vektördür.

Karşıtdeğişkin ve eşdeğişkenin bu formülasyonu burada bu uygulamalar içinde daha doğal sıklıktadır ve tanjant vektörler veya kotanjant vektörler olarak yaşayan üzerinde bir koordinat uzayıdır (bir manifold).Bir xⁱ manifold üzerinde verilen bir yerel koordinat sistemi, koordinat sistemi için başvuru eksenleri vektör alanıdır

${\displaystyle X_{1}={\frac {\partial }{\partial x^{1}}},\dots ,X_{n}={\frac {\partial }{\partial x^{n}}}.}$

Bu koordinat yamasının her noktasında f = (X₁,...,X_n) çerçeveye açar. Eğer yⁱ farklı bir koordinat sistemi ve

${\displaystyle Y_{1}={\frac {\partial }{\partial y^{1}}},\dots ,Y_{n}={\frac {\partial }{\partial y^{n}}},}$

ise f' çerçevesi f çerçevesiyle koordinat ötelemesinin Jacobian matrisinin tersi ile ilişkilidir :

${\displaystyle \mathbf {f} '=\mathbf {f} J^{-1},\quad J=\left({\frac {\partial y^{i}}{\partial x^{j}}}\right)_{i,j=1}^{n}.}$

Veya, indisleri içinde,

${\displaystyle {\frac {\partial }{\partial y^{i}}}=\sum _{j=1}^{n}{\frac {\partial x^{j}}{\partial y^{i}}}{\frac {\partial }{\partial x^{j}}}.}$

Bir tanjant vektör bir vektör tanımı iledir ve bu ${\displaystyle \partial /\partial x^{i}}$ koordinat parçalarının bir doğrusal bileşimidir. Böylece bir tanjant vektör şununla tanımlanır

${\displaystyle v=\sum _{i=1}^{n}v^{i}[\mathbf {f} ]X_{i}=\mathbf {f} \ \mathbf {v} [\mathbf {f} ].}$

Böylece bir vektör çerçevenin değişme sırasıyla karşıtdeğişkinidir.Koordinat sistemi içindeki değişikliği altında, tek olan

${\displaystyle \mathbf {v} [\mathbf {f} ']=\mathbf {v} [\mathbf {f} J^{-1}]=J\,\mathbf {v} [\mathbf {f} ].}$

Bu nedenle teğet vektörün bileşenleri ile dönüşümü

${\displaystyle v^{i}[\mathbf {f} ']=\sum _{j=1}^{n}{\frac {\partial y^{i}}{\partial x^{j}}}v^{j}[\mathbf {f} ].}$

Buna göre, diğerine tek koordinat sisteminden bir karşıtdeğişinti vektörü üzerinden geçen bu yol içinde bu koordinat dönüşümü üzerinden bağlı vⁱ miktarda n in bir sistemi denir.

Bir metrik ile bir vektörün eşdeğişkin ve karşıtdeğişkin bileşenleri

Bir vektör uzayında V içinde bir K alanı üzerinde bir çiftdoğrusal forum ile g : V × V → K (burada metrik tensör olana başvurulabilir), burada eşdeğişkin ve karşıtdeğişkin vektörler arasında fark azdır,çünkü çiftdoğrusal forum sağlayan eşvektörler vektörler ile belirleniyor.Bu,bir v vektör eşsizce belirlenen tüm w vektörleri için bir eşvektör α yoluyladır

${\displaystyle \alpha (w)=g(v,w)}$

Karşıt olarak, her eşvektör α bu denklem ile bir eşsiz v vektör ile belirlenir.Çünkü eşvektörler ile vektörlerin bu kimliği, tek eşdeğişkin bileşenleri'nin veya bir vektörün karşıtdeğişkin bileşenleri olarak konuşabilir olan budur, bunlar, karşılıklı kullanılan bazlar aynı vektörün sade gösterimleridir

verilen bir V tabanı f = (X₁,...,X_n), bu bir eşsiz karşılıklı tabandır ve V nin f^# = (Y¹,...,Yⁿ) gerektireni ile belirlenir.

${\displaystyle Y^{i}(X_{j})=\delta _{j}^{i},}$

Kronecker delta. bu tabanın terimleri içinde, herhangi v vektörü iki yollar içinde yazılabilir:

${\displaystyle {\begin{aligned}v&=\sum _{i}v^{i}[\mathbf {f} ]X_{i}=\mathbf {f} \,\mathbf {v} [\mathbf {f} ]\\&=\sum _{i}v_{i}[\mathbf {f} ]Y^{i}=\mathbf {f} ^{\sharp }\mathbf {v} ^{\sharp }[\mathbf {f} ].\end{aligned}}}$

vⁱ[f] bileşenleri f tabanı içinde v vektörünün eşdeğişkin bileşenleridir, ve v_i[f] bileşenleri f tabanı içinde v nin eşdeğişkin bileşenleridir. Terminoloji bunun için tabanın bir değişimi altında sadeleştiriliyor,

${\displaystyle \mathbf {v} [\mathbf {f} A]=A^{-1}\mathbf {v} [\mathbf {f} ],\quad \mathbf {v} ^{\sharp }[\mathbf {f} A]=A^{T}\mathbf {v} ^{\sharp }[\mathbf {f} ].}$

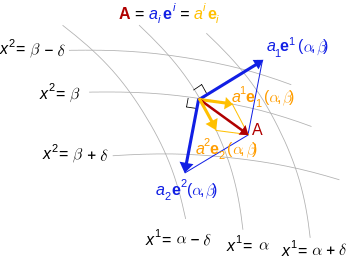
Öklid düzlemi

Öklid düzlemi içinde, vektörlerin nokta çarpımını sağlayan eşvektörler özdeş olsun .Eğer ${\displaystyle \mathbf {e} _{1},\mathbf {e} _{2}}$ bir taban, ise ${\displaystyle \mathbf {e} ^{1},\mathbf {e} ^{2}}$ çift tabanıdır, aşağıdakiler için yeterlidir

${\displaystyle {\begin{aligned}\mathbf {e} ^{1}\cdot \mathbf {e} _{1}=1,&\quad \mathbf {e} ^{1}\cdot \mathbf {e} _{2}=0\\\mathbf {e} ^{2}\cdot \mathbf {e} _{1}=0,&\quad \mathbf {e} ^{2}\cdot \mathbf {e} _{2}=1.\end{aligned}}}$

Böylece, 'e¹ ve e₂ birbirine diktir,e² ve e₁, ve e¹ ve e² nin ve e₁ ve e₂,nin uzunluğu sırasıyla yine normalize edilir.

Örnek

Örneğin,^[2] varsayalımki bizim e₁, e₂ vektörlerimizin verilen bir tabanının bir çiftinin oluşturduğu birbiriyle 45° açı yapıyor, böylece e₁ 2 uzunluğu var ve e₂ 1 uzunluğu var.Daha sonra, aşağıdaki gibi ikili bir baz vektörleri verilmiştir:

• e² bir 90° açının aracılığıyla e₁ dönmesinin sonuçlarıdır(varsayımsal olarak) e₁, e₂ çifti pozitif eğilimli olur),ve sonra yeniden ölçeklendirilmesi ile e²•e₂ = 1 tutulur.
• e¹ bir 90° açının aracılığıyla e₂ dönmenin sonuçlarıdır ve sonra yeniden ölçeklendirilmesi ile e¹•e₁ = 1 tutulur.

Bu kurallar uygulanarak,

${\displaystyle \mathbf {e} ^{1}={\frac {1}{2}}\mathbf {e} _{1}-{\frac {1}{\sqrt {2}}}\mathbf {e} _{2}}$ buluruz ve

${\displaystyle \mathbf {e} ^{2}=-{\frac {1}{\sqrt {2}}}\mathbf {e} _{1}+2\mathbf {e} _{2}.}$

Böylece karşılıklılık esasına göre orijinal bazda gidiş içinde temel matrisin değişimi

${\displaystyle R={\begin{bmatrix}1/2&-1/{\sqrt {2}}\\-1/{\sqrt {2}}&2\end{bmatrix}},}$

nedeniyle

${\displaystyle [\mathbf {e} ^{1}\ \mathbf {e} ^{2}]=[\mathbf {e} _{1}\ \mathbf {e} _{2}]{\begin{bmatrix}1/2&-1/{\sqrt {2}}\\-1/{\sqrt {2}}&2\end{bmatrix}}.}$

Örneğin, vektör

${\displaystyle v={\frac {3}{2}}\mathbf {e} _{1}+2\mathbf {e} _{2}}$ dir ve bir vektör karşıtdeğişir bileşenleri ile

${\displaystyle v^{1}={\frac {3}{2}},\quad v^{2}=2.}$ eşdeğişken bileşenleri v vektörü için denkliğin iki bağıntısı ile elde ediliyor:

${\displaystyle v=v_{1}\mathbf {e} ^{1}+v_{2}\mathbf {e} ^{2}=v^{1}\mathbf {e} _{1}+v^{2}\mathbf {e} _{2}}$ böylece

${\displaystyle {\begin{aligned}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}&=R^{-1}{\begin{bmatrix}v^{1}\\v^{2}\end{bmatrix}}\\&={\begin{bmatrix}4&{\sqrt {2}}\\{\sqrt {2}}&1\end{bmatrix}}{\begin{bmatrix}v^{1}\\v^{2}\end{bmatrix}}={\begin{bmatrix}6+2{\sqrt {2}}\\2+3/{\sqrt {2}}\end{bmatrix}}\end{aligned}}.}$

Üç-boyutlu Öklid uzayı

Üç boyutlu Öklid uzayda,ayrıca bir zorunlu olarak ne dikey ne de birim norm varsayımı değildir.E₃ün verilen bir e₁, e₂ e₃ taban vektörlerinin kümesi açıkça çift taban olarak belirlenebilir.Karşıtdeğişken(dual) taban vektörleri:

${\displaystyle \mathbf {e} ^{1}={\frac {\mathbf {e} _{2}\times \mathbf {e} _{3}}{\mathbf {e} _{1}\cdot (\mathbf {e} _{2}\times \mathbf {e} _{3})}};\qquad \mathbf {e} ^{2}={\frac {\mathbf {e} _{3}\times \mathbf {e} _{1}}{\mathbf {e} _{2}\cdot (\mathbf {e} _{3}\times \mathbf {e} _{1})}};\qquad \mathbf {e} ^{3}={\frac {\mathbf {e} _{1}\times \mathbf {e} _{2}}{\mathbf {e} _{3}\cdot (\mathbf {e} _{1}\times \mathbf {e} _{2})}}.}$

e_i ve eⁱ çifti ortonormal değildir,bu hala karşılıklı ikilidir:

${\displaystyle \mathbf {e} ^{i}\cdot \mathbf {e} _{j}=\delta _{j}^{i},}$

O zaman herhangi vektör v nin karşıtdeğişkin koordinatlaarı v nin nokta çarpımı ile elde edilebilir ve karşıtdeğişkin taban vektörleri ile:

${\displaystyle q^{1}=\mathbf {v} \cdot \mathbf {e} ^{1};\qquad q^{2}=\mathbf {v} \cdot \mathbf {e} ^{2};\qquad q^{3}=\mathbf {v} \cdot \mathbf {e} ^{3}.\,}$

aynı şekilde, v nin eşdeğişken bileşenleri v nin nokta çarpımından eşdeğişkin taban vektörleri ile elde edilebilir, viz.

${\displaystyle q_{1}=\mathbf {v} \cdot \mathbf {e} _{1};\qquad q_{2}=\mathbf {v} \cdot \mathbf {e} _{2};\qquad q_{3}=\mathbf {v} \cdot \mathbf {e} _{3}.\,}$

İse v iki (karşılıklı) yolla ifade edilebilir, viz.

${\displaystyle \mathbf {v} =q_{i}\mathbf {e} ^{i}=q_{1}\mathbf {e} ^{1}+q_{2}\mathbf {e} ^{2}+q_{3}\mathbf {e} ^{3}\,}$

veya

${\displaystyle \mathbf {v} =q^{i}\mathbf {e} _{i}=q^{1}\mathbf {e} _{1}+q^{2}\mathbf {e} _{2}+q^{3}\mathbf {e} _{3}.\,}$

elimizde yukarıdaki ilişkileri birleştiren ki

${\displaystyle \mathbf {v} =(\mathbf {v} \cdot \mathbf {e} _{i})\mathbf {e} ^{i}=(\mathbf {v} \cdot \mathbf {e} ^{i})\mathbf {e} _{i}\,}$

ve biz karşıtdeğişkin tabanına eşdeğişkin dönüştürebiliriz

${\displaystyle q_{i}=\mathbf {v} \cdot \mathbf {e} _{i}=(q^{j}\mathbf {e} _{j})\cdot \mathbf {e} _{i}=(\mathbf {e} _{j}\cdot \mathbf {e} _{i})q^{j}\,}$

ve

${\displaystyle q^{i}=\mathbf {v} \cdot \mathbf {e} ^{i}=(q_{j}\mathbf {e} ^{j})\cdot \mathbf {e} ^{i}=(\mathbf {e} ^{j}\cdot \mathbf {e} ^{i})q_{j}.\,}$

eşdeğişken koordinatların indisleri, vektörleri ve tensörlerin indisleri vardır.Eğer eşdeğişken taban vektörleri ortonormal ise bu eşdeğişkin taban vektörlerine eşdeğerdir, böylece bu eşdeğişkin ve karşıtdeğişkin koordinatlar arasında ayrıma gerek yoktur.

Genel Öklid uzayı

Daha genel olarak,bir n-boyutlu Öklid uzayı V içinde, eğer bir taban

${\displaystyle \mathbf {e} _{1},\dots ,\mathbf {e} _{n}}$,ise

karşılıklı taban ile veriliyor

${\displaystyle \mathbf {e} ^{i}=e^{ij}\mathbf {e} _{j}}$

burada e^ij katsayısı matrisin tersinin girişidir

${\displaystyle e_{ij}=\mathbf {e} _{i}\cdot \mathbf {e} _{j}.}$

Yani, O zaman elimizde

${\displaystyle \mathbf {e} ^{i}\cdot \mathbf {e} _{k}=e^{ij}\mathbf {e} _{j}\cdot \mathbf {e} _{k}=e^{ij}e_{jk}=\delta _{k}^{i}.}$

Herhangi vektörlerin eşdeğişkin ve karşıtdeğişkin bileşenleri

${\displaystyle \mathbf {v} =q_{i}\mathbf {e} ^{i}=q^{i}\mathbf {e} _{i}\,}$

yukarıdaki ile ilişkili olarak

${\displaystyle q_{i}=\mathbf {v} \cdot \mathbf {e} _{i}=(q^{j}\mathbf {e} _{j})\cdot \mathbf {e} _{i}=q^{j}e_{ji}}$

ve

${\displaystyle q^{i}=\mathbf {v} \cdot \mathbf {e} ^{i}=(q_{j}\mathbf {e} ^{j})\cdot \mathbf {e} ^{i}=q_{j}e^{ji}.\,}$

Resmi olmayan genel

fizikte alanlar konusunda,eşdeğişken sıfatı sıklıkla değişken için bir sinonim olarak resmi olmadan kullanılır. Örneğin, Schrödinger denkleminin özel görelilik koordinat dönüşümleri altında yazılan formu tutmaz.Böylece, bir fizikçi Schrödinger denklemi eşdeğişken değil diyebilir. Buna karşılık, Klein-Gordon denklemi ve Dirac denklemi Bu koordinat dönüşümleri altında yazılı şeklini korur. Böylece, bir fizikçi bu denklemler eşdeğişken olduğunu söyleyebilirsiniz.

"Eşdeğişken"nin geneline rağmen,bu Klein-Gordon ve Dirac denklemleri değişmez olduğunu ve Schrödinger denkleminin değişmez olmadığını söylemek daha doğru olur. toplanırlık, belirsizliği kaldırmak için, değişmezliği değerlendirilir kılan dönüşüm gösterilmelidir.

Vektörlerinin bileşenleri karşıtdeğişken ve eşvektörler olanlar eşdeğişken olduğu için, vektörlerin kendileri de karşıtdeğişkin ve eşdeğişkin gibi eşvektörler olarak adlandırılır.

geri çekme - difeomorfizm altında karşıtdeğişkin ve eşvektörler - difeomorfizm altında eşdeğişkindir- Bu kullanım vektörleri beri ileri itme ancak yanıltıcı olabilir .

Bak Einstein gösterimi ayrıntıları için.

Tensör analizinde kullanım

Eşdeğişir ve zıtdeğişir arasındaki ayrım tensörler ile hesaplamalarda özel önemli taşır, bunun için sıklıkla karışıkdeğişkin denir.Bunun anlamı hem eşdeğişkin ve hem de karşıtdeğişkin veya hem vektör ve hemde ikili vektör bileşenleri var.Bir tensörün değeri değişkin ve eşdeğişkin terimlerinin sayılarıdır, ve Einstein gösterimi içinde, eşdeğişkin bileşenlerin alt indisler varken karşıtdeğişkin bileşenlerin üst indisler vardır. İkilik eşdeğişkin ve karşıtdeğişkin arasına müdahele edildiğinde bir vektör veya tensör nicelik bileşenleri modern diferansiyel geometri kullanıl rağmen tensör gösteriminde serbest-indeks metotları daha felsefidir.

Tensör analizinde, bir eşdeğişkin vektör çeşitleri more veya bir karşıtdeğişkin vektör karşılığına karşılıksızlıktır.Uzunluklar için bağıntılar, alanlar ve vektör uzayı içinde nesnelerin hacimleri eşdeğişkin ve karşıtdeğişkin indisleri ile tensörlerin terimleri içinde verilebilir. Koordinatların basit açılması ve büzülmesi altında , karşılıklılık tamdır; karıştırılmış bir vektörün bileşenleri afin dönüşümü altında eşdeğişinken ve karşıtdeğişinken bağıntıları arasında gidiyor bir manifold üzerinde,tipik olacak bir tensor alanının iki türden çoğul indisler var.Yaygın olarak izlenen kural tarafından, eşdeğişken indisleri alt indisler olarak yazılıyor, oysa eşdeğişinken indisler alt indislerdir.Eğer manifold is donanım ile bir metrik, eşdeğişken ve karşıtdeğişken indisler birbirine çok yakından ilişki alır.Büzülme tarafından karşıtdeğişken indisler eşdeğişken indisler metrik tensör ile dönüşebilir.Terslik metrik tensörün tersinin (matris) büzülmesi ile olasıdır. Genel olarak, böyle bir ilişki bir metrik tensörde uzay içinde böyle bir ilişki olmadığını unutmayın.Ayrıca, daha soyut bir bakış açısıyla, bir tensör ya da türün bileşenleri basitçe "burada" ve seçilen koordinatlar üzerinde yalnızca hesaplanabilir kalıntılar böyle bağlı değerlerdir

Geometrik terimlerin içinde açıklama genel bir tensör karşıdeğişken indisleri gibi eşdeğişken indislerine sahip olmasıdır.Çünkü bu hem tanjant demet hem de kotanjant demet içinde diri parçalar olarak var.

Bir karşıtdeğişinken vektörü tek bu ${\displaystyle {\frac {dx^{\mu }}{d\tau }}}$ dönüşümü gibidir, burada ${\displaystyle x^{\mu }\!}$ ifadesi ${\displaystyle \tau \!}$ uygun zamanında bir parçacığın koordinatlarıdır.Bir eşdeğişinken vektörü ${\displaystyle {\frac {\partial \phi }{\partial x^{\mu }}}}$ dönüşümleri gibidir, burada ${\displaystyle \phi \!}$ bir skaler alandır.

Cebir ve geometri

Buradaki kategori teorisi içinde olanlar eşdeğişkin funktorlar ve karşıtdeğişkin funktorlardır.Bir vektör uzayının ikili uzayı bir karşıtdeğişkin funktörün standart bir örneğidir.Çokludoğrusal cebirin bazı yapıları 'karışık' değişkindir, funktör olmaktan alıkoyan budur.

Geometride,aynı iç gönderme/dış gönderme ayrımı yapıların değişkenliğinin değerlendirilmesinde faydalıdır.Bir düzgün manifold M e bir tanjant vektör başlangıçta M içine düzgün bir eğri gönderme ve verilen bir P noktası aracılığıyla geçiyor. Bu bunun için M in düzgün göndermeleri sırasıyla eşdeğişkindir.Bir karşıtdeğişkin vektör,veya 1-form,reel eksene M den bir düzgün göndermeyle yapılan P yakınındaki aynı yoldur.Bu kotanjant demet içindedir, tanjant uzayının ikili uzayından inşa edilir sırasıyla dx_i bileşenleri tek- formun bir yerel taban eşdeğişkini olacak; ama tek-formlar ve genel içinde diferansiyel formun geri çekme düzgün göndermeleri altında karşıtdeğişkindir,uygulama için bu çok önemlidir ; örneğin bir diferansiyel form herhangi altmanifoldla sınırlı olabilirken,bu tanjant vektörler için aynı bir alan mantıklı değildir.

Eşdeğişkin ve karşıt-değişkin bileşenlerin dönüşümü koordinat dönüşümleri altında farklı yollar içindedir.Bir manifold üzerinde bir gönderimin manifoldun kendisi üzerine bir koordinat dönüşümü dikkate alınarak ,bir tensörün eşdeğişkin indislerinin dönüşüm özellikleri bir geri çekme ile ve karşıtdeğişken indislerinin dönüşüm özellikleri ise bir ileri itme ile veriliyor.

Ayrıca bakınız

• Eşdeğişkin dönüşümü
• Tabanın değişimi
• Aktif ve pasif dönüşüm
• İki nokta tensör tensörler için genelleştirilmiş bu gösterim asli ve çift uzay içinde değil ama diğer vektör uzayları içinde var (aynı manifold üzerinde diğer tanjant uzaylar gibi ).
• Karışık tensör

Notlar

1. Bir taban Rⁿ den Vye bir doğrusal izomorfizm olarak f burada kazançlı görülebilir.Bir satır vektörü girişleri olarak f,ilişkili tabanın ögeleriyle ilişkili doğrusal izomorfizm ise ${\displaystyle \mathbf {x} \mapsto \mathbf {f} \mathbf {x} .}$

Kaynakça

1. J.A. Wheeler, C. Misner, K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. ISBN 0-7167-0344-0. 
2. Bowen, Ray (2008). "Introduction to Vectors and Tensors". Dover. ss. 78, 79, 81. http://repositories.tamu.edu/bitstream/handle/1969.1/2502/IntroductionToVectorsAndTensorsVol1.pdf?sequence=12. 

• Arfken, George B.; Weber, Hans J. (2005), Mathematical Methods for Physicists (6th bas.), San Diego: Harcourt, ISBN 0-12-059876-0 .
• Dodson, C. T. J.; Poston, T. (1991), Tensor geometry, Graduate Texts in Mathematics, 130 (2nd bas.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-52018-4, MR 1223091 .
• Greub, Werner Hildbert (1967), Multilinear algebra, Die Grundlehren der Mathematischen Wissenschaften, Band 136, Springer-Verlag New York, Inc., New York, MR 0224623 .
• Sternberg, Shlomo (1983), Lectures on differential geometry, New York: Chelsea, ISBN 978-0-8284-0316-0 .
• Sylvester, J.J. (1853), "On a Theory of the Syzygetic Relations of Two Rational Integral Functions, Comprising an Application to the Theory of Sturm's Functions, and That of the Greatest Algebraical Common Measure", Philosophical Transactions of the Royal Society of London (The Royal Society) 143: 407–548, DOI:10.1098/rstl.1853.0018, JSTOR 108572 .

Dış bağlantılar

• Hazewinkel, Michiel, ed. (2001), "Covariant tensor", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104, http://eom.springer.de/p/c026880.htm 
• Hazewinkel, Michiel, ed. (2001), "Contravariant tensor", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104, http://eom.springer.de/p/c025970.htm 
• Eric W. Weisstein, Covariant Tensor (MathWorld)
• Eric W. Weisstein, Contravariant Tensor (MathWorld)
• Invariance, Contravariance, and Covariance

Şablon:Tensors