Kutu grafiği

Michelson-Morley Deneyi veri setleri için dikey "Kutu Grafikleri"

İstatistik biliminde kutu grafiği (İngilizce: Box plot) bir betimsel istatistik ve istatistiksel grafik aleti olup niceliksel verileri görsel şekilde özetlemek için Amerikan istatistikçi John Tukey tarafından kutu-ve-bıyıklar grafiği adı altında bir açıklayıcı veri analizi aracı olarak ilk defa geliştirilmiştir. Kutu grafiği, ilgili değişken bakımından veri için hazırlanan beş sayılı özetleme tablosu ^[1] gösterimini grafiksel olarak özetlemeye dayalıdır. Özellikle merkezsel konum, yayılma, çarpıklık ve basıklık yönünden verileri özetlemek ve aykırı değerleri tanımlamak için kullanılır.

En basit çiziminde izlenecek yordam

1. Veri seti için X_med: medyan (ortanca), X_min (en küçük gözlem değeri), Q1 (birinci dörttebirlik), ve Q3 (üçüncü dörttebirlik) ve X_maks(en büyük gözlem değeri) olarak bulunur. Bunun en kolay yaklaşımı veri setinin en küçük değerden en büyük değere kadar sıralaması yapılmasi ve bu sıralamadan beş sayılı özetleme tablosu çıkarılmasıdır; yani şu tablo verilebilir:

            X_med

        Q1         Q3

   X_min                X_maks

2. Kutu grafiği iskeleti, veri minimum ile maksimum değerleri arasında üzeri ölçekli bir çizgiden oluşur; yani X_min lle X_maks noktaları arasında ya yatay ya da dikey bir çizgi halindedir.

3. Bu çizgi üzerinde ölçeğe göre bir kutu çizilir. Kutunun en küçük değeri birinci dörttebirlik Q1 ve en büyük değeri üçüncü dörttebirlik Q3 olur. Kutunun uç noktalarına Tukey tarafından "menteşe" adı verilmiştir; yani Q1, ve Q3 kutunun uç noktaları "menteşe" noktalarıdır. Bu kutunun uzunluğu QA = Q3 - Q1 olur ve bu QA verinin çeyrekler açıklığı ölçüsünu gösterir. Dikkat edilirse böylece gösterim bir "kutu" ile dörttebirlikler dışındaki (yani "menteşe" dışındakı) veri değerlerini gösteren "bıyıklar" şekile girmiştir. Bunun için bu grafiğe John Tükey tarafından kutu-ve-bıyıklar grafiği adı verilir.

4. Medyan "kutu"nun içinde ölçeğe göre yerine konulup işaretlenir.

Yorumlanması

Veri setinin niteliklerini bir kutu grafiği görsel şekilde ifade eder:

• Merkezsel konum: Verinin merkezsel konumu kutunun içinde işaretlemiş olan medyan noktası ile gösterilir.
• Yayılma: Verinin yayılmasının açıklık ölçüsüyle ölçülen niteliği, "kutu grafiği"'nin (yatay veya dikey) tüm çizgisi ile görülür. Çeyrekler açıklığı ise "kutu grafiği"nde kutunun büyüklüğü ile görülür.
• Şekil:
  • Çarpıklık: Verinin "çarpıklık" ölçüsü bu grafikte bulunmaz. Ama verinin çarpıklık karakteri kutunun tüm çizginin küçük X_min tarafına mı yoksa büyük X_maks tarafına mı yakın olması ile görülür. Eğer kutu, çizginin küçük tarafında ise, kutu içindeki medyan noktası X_min değerine yakın olur ve kutu dışında kalan çizginin yüksek kısmı (yani X_maksa doğru kısmı) pozitife doğru uzunca bir kuyruk gösterir. Bu demektir ki veri pozitif çarpıklık niteliği gösterir. Eğer kutu, çizginin büyük tarafında ise, yani medyan noktası X_maks değerine yakın ise, kutu dışında kalan çizginin düşük kısmı (yani X_mine doğru kısmı) negatife doğru uzun kuyruklu olur ve böylece veri değerleri negatif çarpıklık gösterir. Ancak "çarpıklık" karakterini doğrudan doğruya ölçen bir sayısal ölçü "kutu grafiği"nden hemen doğrudan doğruya çıkmaz.
  • Basıklık: Yine basıklık ölçüsü bu grafikte yoktur. Ama verinin basıklık niteliği hakkında bu grafikten bir kanaat edinilebilir. Dikkat edilirse bu kanaat edinme olup, epeyce zayıf, bir intiba edinme şekilindedir ve tam olarak basıklık niteliği öğrenilmez. Basıklık için bir kanaat sağlama kutunun genişliği ile çizginin genişliğini karşılaştırılma ile edinelebilir. Eğer kutu çizginin çoğunu kapsıyorsa genellikle verinin basık olduğu hakkında bir ilk intiba ortaya çıkabilir.

Alternatif şekiller

Aykırı değer sorunları ve kutu grafiği

Eğer veri sıralaması sonunda ya diğer değerlerden çok küçük veya diğer değerlerden çok büyük uç değer bulunmaktaysa kutu grafiği için bu problem olabilir. Bu çok değişik uç değerler bıyık çizgilerini çok uzun yapıp, geri kalan verilerin birbirine çok yakın olmalarına, hatta birbirleri ile çakışmalarına, neden olabilir. Bu nedenle alternatif kutu grafikleri kullanılabilir ve bu alternatifle uç noktalarının minimum ve maksimum veri değerlerinden diğer değerler olmasına dayanır. Şu alternatifler kullanılmıştır:

• Uç noktalarının kutu uçlarından 1,5 kutu genişliğe (yani 1.5 x "çeyrek aralığı") kadar uzatılması;
• Uç noktaları veri aritmetik ortalama etrafında ortalama değerinden 1 standart sapma altına ve üstüne uzatılması;
• Uç noktalarının 9'uncu yüzdebirlik ile 91'inci yüzdebirlik olması;
• Uç noktalarının 2'inci yüzdebirlik ile 98'inci yüzdebirlik olması;

Bu şekillerde değişik uç noktası kullanıldığı zaman aykırı değerler özel olarak çizginin dışında, çok kere ölçeğe uymadan, birer nokta (veya boş nokta veya küçük yıldız veya *) halinde gösterilmeleri tavsiye edilmektedir.

Çentikli kutu grafiği

Bu halde kutu grafiğinde (çok kere kutu içinde medyan noktasının hemen yanında) bir veri aritmetik ortalama noktası konulmakta ile %95 (hatta %99) güven aralığı alt ve üst sınırları da birer "çentik (notch)" olarak çizgi üzerine konulmaktadır. Bu yaklaşım ile bir betimsel istatistik gösterim aracı olan kutu grafiği üzerine bir çıkarımsal istatistik (yani güven aralığı) eklenmiş olmakta ve kutu grafiğinin temelden karakteri değiştirilmektedir. Bir "çentikli kutu grafiği" çok kere bir çeşit çıkarımsal analiz aracı olarak aykırı değerlerin tanımlanması için kullanılmaktadır. Bazen kutu uçlarından çentiklere kadar "kalın bıyıklar" çizilmektedir.

Diğer yaklaşımlar

Kutu grafiğinin çeşitli diğer alternatifleri de bulunmaktadır ve bunlar burada hiç kritik görmeden şöyle sıralanabilir:

• Bazen kutu grafikleri ya bir çubuk olarak ya da bir çizgi olarak verilip sadece bunlar üzerinde beş nokta ayrıca yazılarak gösterilir.
• Bazen %2, %9, %91, %98 gibi beklemedik yüzdebirlikler de (%25, %50 ve %75 yüzdebirliklerle birlikte) yedi nokta olarak özel olarak gösterilmektedir. Eğer veri bir normal dağılım gösterirse bu 7 yüzdebirlik birbirlerinden eşit aralıklarla ayrılması gerekmektedir. Böylece kutu grafiği bir normal dağılıma uygunluk testi için parametrik olmayan sınama (uyma uygunluğu sınaması) aleti olarak kullanılmaktadır.

Örnekler

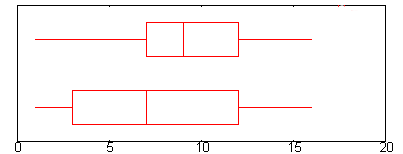
Ör.1./ İki örneklem veri seti için şu "Beş sayılı özetleme tablosu" verilmiş ve şu iki yatay "kutu grafiği" çizilmiştir:

Örneklem 1 (üstte) : X_min=1 , Q1= 7, X_med= 9 , Q3 = 12 , X_maks = 16.

Örneklem 2 (altta) : X_min=1 , Q1= 3 , X_med= 7 , Q3 = 12 , X_maks = 16.

Ör.2./ Bir tüketim malı için yapılan yarışmaya cevap kuponu gönderenlerin yaşları şöyledir:

23, 21, 10, 15, 12, 15, 39, 17, 21, 30, 18, 20

Bu veri setinin en küçükten en büyüğe sıralanması şöyle elde edilir:

10, 12, 15, 15, 17, 18, 20, 21, 21, 23, 30, 39

"Beş sayılı özetleme tablosu" şöyle bulunur:

            19

        15        22

   10               39

Şu yatay kutu grafiği çizilmiştir:

      +---+--+
  ----|   +  |--------        *
      +---+--+

-+----+----+----+----+----+----+- Yaş
10   15   20   25   30   35   40

Not: 39 tam bir "aykırı değer" olduğu için tek başına bir nokta halinde (*) ile gösterilir.

Kaynakça

1. "Beş sayılı özetleme tablosu" minimum. birinci dörttebirlik, medyan (ortanca), üçüncü dörttebirlik ve maksimum değerlerinin ya bir sıra halinde ya da medyan en üstte ortada, dörttebirlikler ikinci satırda medyan yanlarında ve manimum ve maximum üçüncü satırda en dışarıda yazılarak elde edilen tablodur.

• İngilizce Wikipedia "Box_plot" maddesi (İngilizce) (Erişme:14.5.2010)

Ayrıca bakınız

• John Tukey
• Açıklayıcı konum ölçüleri
• Çoklu sayılı özetleme tabloları

Dış kaynaklar

• Tukey, John W. (1977), Exploratory Data Analysis (Açıklayıcı Veri Analizi). Reading MA.:Addison-Wesley (İngilizce)
• McGill, R., John W. Tukey ve Wayne A. Larsen. (1978) "Variations of Box Plots". The American Statistician, Cilt.32(1), say.12-16. (İngilizce) (Erişme:14.5.2010).
• "Kutu Grafiği" çizmek iin Microsoft Excel Kutuçizim kullanılması (İngilizce) (Erişme:14.5.2010).